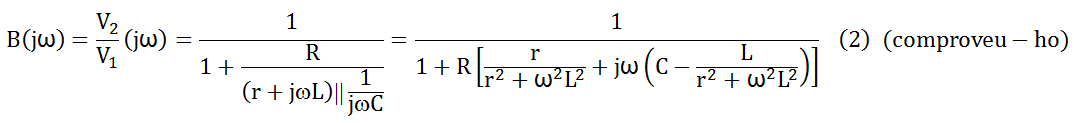En l'anterior pràctica Oscil·ladors sinusoïdals (1) , el valor absolut del factor d'estabilitat de la freqüència és |SF| = 2/3. A continuació utilitzarem una altra xarxa de realimentació que permet obtenir valors de |SF| molt més alts. La topologia d'aquesta nova xarxa és, simplement, un divisor de tensió, com s'indica a la fig. 1 .
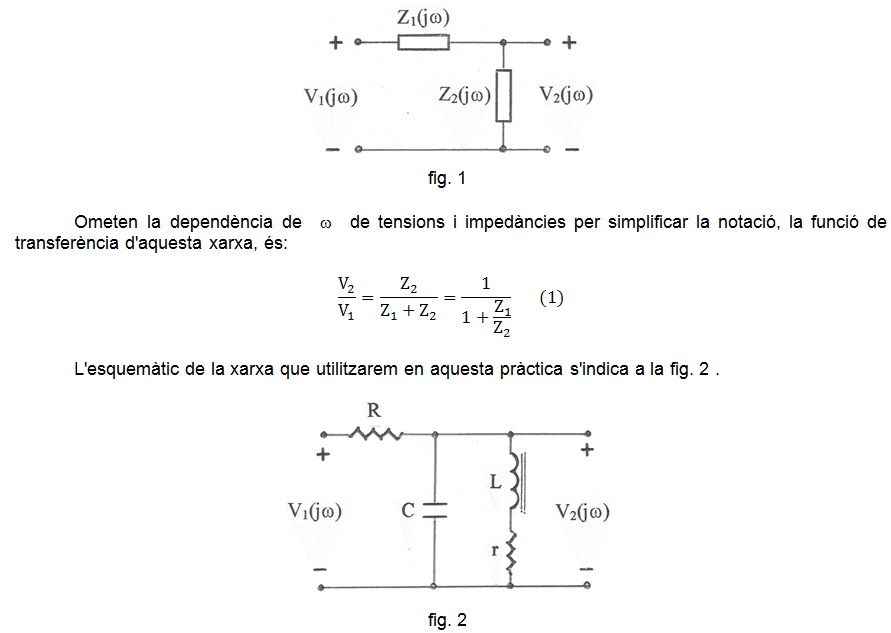
r representa la resistència equivalent en sèrie de les pèrdues de la bobina -resistència del conductor amb el que està construïda i les pèrdues en el nucli. La funció de transferència és, doncs:
Igualant a zero la part imaginària del denominador de la (2), trobem la freqüència ω0 a la qual la funció de transferència és un nombre real, és a dir, la freqüència a la qual V2 està en fase amb V1 -ressonància-, la qual cosa, juntament amb un amplificador de guany real i positiu A , fa aquesta xarxa utilitzable per fer un oscil·lador de freqüència ω0 :
i la (6) ens diu que a ω0 la xarxa es comporta com un divisor de tensió resistiu on Re = L/rC és la resistència equivalent de pèrdues de la bobina en paral·lel amb aquesta -raoneu-ho. S'haurà observat que es considera el condensador com un element ideal -sense pèrdues.
Així, per fer un oscil·lador de freqüència ω0 , només caldrà fer un sistema realimentat amb un amplificador no inversor -per exemple un AO- de guany:
que seria un sistema marginalment estable, on caldria augmentar una mica més el guany per assegurar l'arrencada i el manteniment de les oscil·lacions en front possibles canvis de valors dels components per envelliment, agents externs com temperatura i/o humitat, etc. -raoneu-ho tot això.
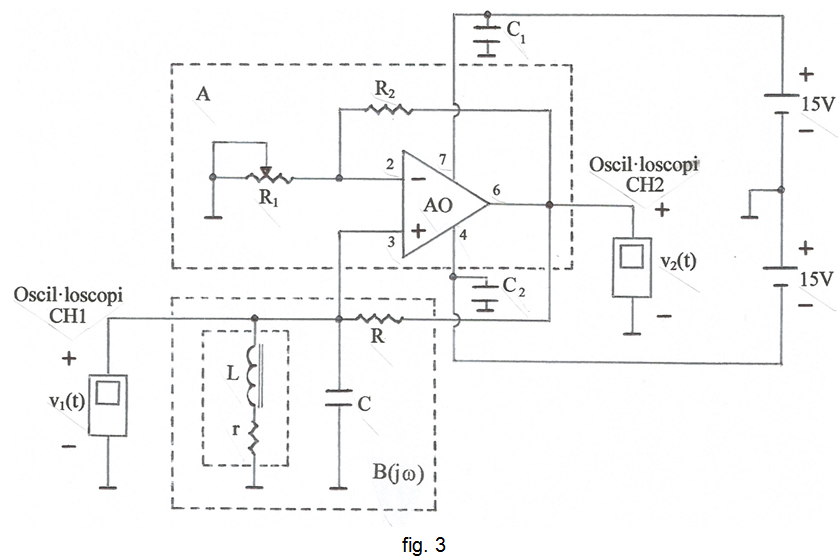
A la fig. 3 s'indica l'esquemàtic del circuit a assajar, on ara s'indiquen com v1(t) la tensió d'entrada a l'amplificador/sortida de la xarxa, i com v2(t) la tensió de sortida de l'amplificador/entrada a la xarxa.
Observeu que el guany de l'AO ve donat per A = 1+ (R2/R1) (9) -raoneu-ho-, el qual es pot variar actuant sobre R1. Llavors, igualant (8) i (9) i separant R1 : R1 = ReR2 / R (10) valor que, pel que abans s'ha dit, s'haurà de disminuir per assegurar el correcte funcionament de l'oscil·lador .
Relació de components:
Les resistències fixes són de 0,25W de dissipació.
Procediment:
• Amb una llima fina poliu els extrems dels terminals de la inductància per poder inserir-la amb més facilitat a la protoboard.
• Amb el multímetre mesureu el valor de la seva resistència. Com que no coneixem la resistència equivalent de pèrdues del nucli, prendrem com a valor per a r solament el valor de la resistència mesurada del conductor. Per poder continuar l'explicació, suposarem que el valor de r és d'uns 40Ω .
• En base als valors nominals dels components i de la mesura anterior, la freqüència de l'oscil·lador hauria de ser, aproximadament:
i substituint els valors nominals dels components a (14) s'obté: |SF| ≅ 86,9 -comproveu-ho-, valor molt més gran que |SF| = 2/3 de l'anterior pràctica: Oscil·ladors sinusoïdals (1) .
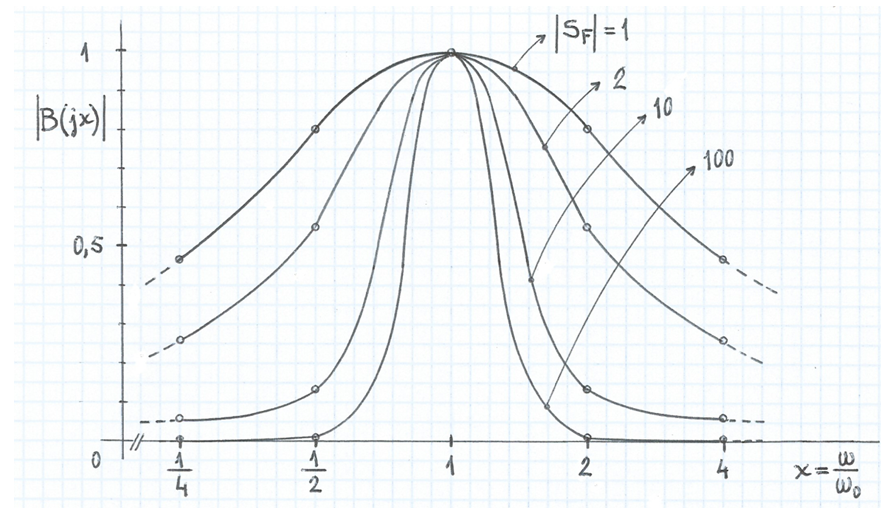
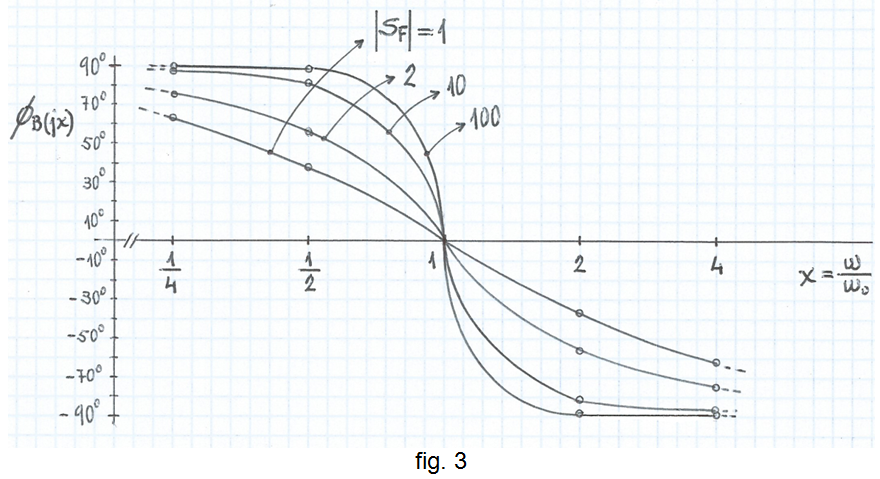
• El guany i la fase de la forma aproximada (13) de B(jω) són:
Observeu que el guany IB(jx)Ι a la freqüència ω0 val 1 , la qual cosa es deu a que hem considerat la bobina i el condensador com elements ideals, és a dir, sense pèrdues, a la fi de simplificar l'anàlisi. Realment, les pèrdues en aquests elements, sobre tot a la bobina, faran que aquest guany sigui inferior a 1 i, en conseqüència, es fa imprescindible un amplificador que aporti un guany superior a 1 per compensar-les i poder implementar així un oscil·lador -raoneu-ho.
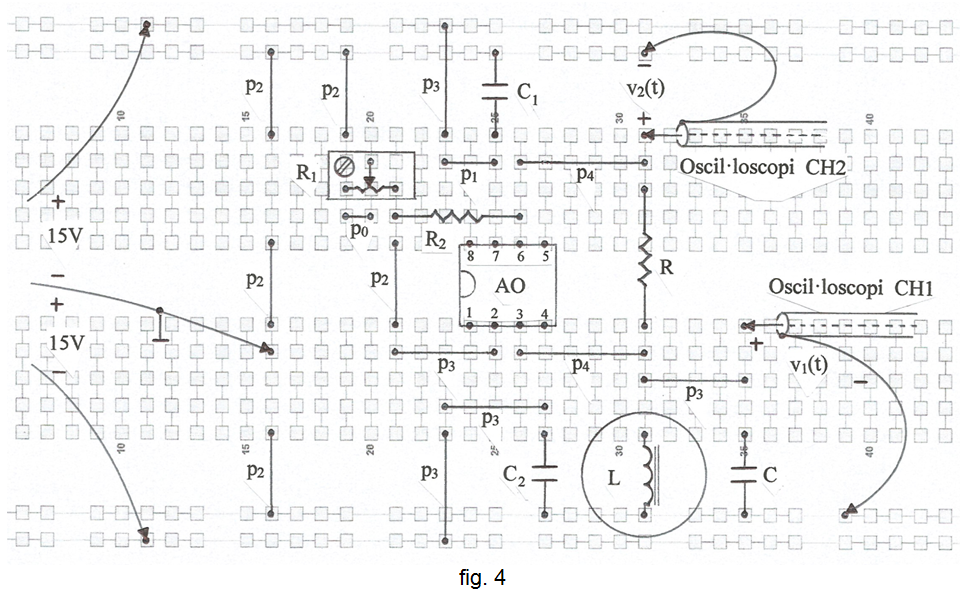
• La planificació del muntatge a la protoboard s'indica a la fig. 4 i a la fig. 5, una fotografia.
• Abans de muntar el circuit mesureu els valors reals dels elements que fixen el valor de la freqüència de l'oscil·lador i, en base a aquests valors, feu una previsió del valor d'aquesta.
• Mesureu el valor real de R2 .
• Abans d'inserir la resistència variable R1 a la protoboard, amb un multímetre ajusteu el seu valor a uns 50kΩ.
• Engegueu la font d'alimentació i amb un tornavís aneu reduint el valor de la resistència variable R1 fins que l'oscil·lador arrenqui. Comproveu que els valors d'aquesta resistència i de la freqüència del senyal obtingut estan sensiblement d'acord amb les previsions teòriques.
• Igual que en la pràctica anterior: Oscil·ladors sinusoïdals (1) , per assegurar l'arrencada i el manteniment de les oscil·lacions, cal disminuir una mica el valor previst per a R1 , la qual cosa comportarà acceptar cert grau de distorsió de la tensió v2(t) -raoneu-ho.
• Comproveu que reduint fins i tot a zero el valor de R1 , amb la qual cosa el senyal v2(t) serà gaire bé un senyal rectangular, el senyal v1(t) manté la seva forma gaire bé sinusoïdal a conseqüència de l'efecte de filtre passabanda de la xarxa de realimentació. Així, si convé, es pot disposar del senyal més pur que hi ha a l'entrada a l'amplificador que no pas a la sortida, la qual cosa dependrà de l'aplicació que es pretengui donar a l'oscil·lador.
• Experimenteu que com més gran és el valor de R , més intensa és l'acció de filtratge de la xarxa, però també cal augmentar el guany de l'amplificador. A més, com més gran és R , el factor d'estabilitat del valor de la freqüència SF també augmenta, segons ens indica (21).
• Proveu amb altres valors de L i C .
• Suggeriment: experimenteu el màxim valor de la freqüència que es pot aconseguir amb aquesta topologia de circuit. Quines limitacions i/o avantatges s'obtenen si es substitueix aquest AO per un altre amb un producte guany×ample de banda diferent?
• Més suggeriments: 1) comproveu que la funció de transferència de la xarxa de la fig. 2 en el domini de s es pot expressar així: