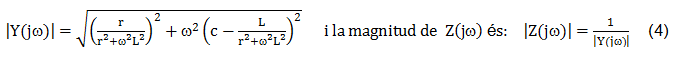Abans de fer aquesta pràctica cal haver fet, o al menys llegit, l'anterior pràctica : Condensadors.

Una inductància es construeix fent una bobina, és a dir, enrotllant un conjunt d'espires de fil conductor, normalment Cu, que poden estar més o menys separades o superposades al voltant d'un nucli, o bé enrotllades sobre un suport sense nucli -el nucli és l'aire.  Degut a aquestes característiques constructives, una inductància real tindrà una resistència paràsita equivalent de pèrdues   r   en sèrie i una capacitat paràsita total equivalent entre espires   c   en paral·lel.  Un model realista d'inductància pot ser, doncs, el que s'indica a la fig. 1. 

 

  

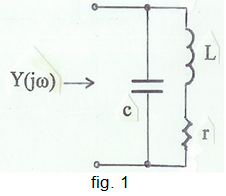
          La importància relativa d'aquests elements paràsits depèn de la freqüència de treball, com es veurà a continuació.

  L'admitància en règim permanent sinusoïdal del model d'inductància de la fig. 1 val:

on es veu que una inductància real presenta una freqüència d'autoressonància   ω_a = 2πf_a   per a la qual   Y(jω_a)   serà real. Igualant a zero la part imaginària de  Y(jω)  trobem   ω_a :

            Separant     r²+ω_a²L²    de (2) i substituint-ho a la part real de  (1):

           La magnitud de  Y(jω)  és:

 

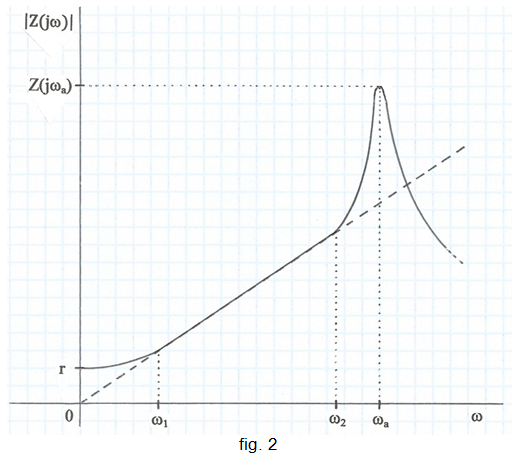
            La representació gràfica de  (4)  té la forma aproximada que s'indica a la fig. 2.

            La recta de traç discontinu correspon al comportament amb la freqüència d'una inductància ideal  L . La gràfica amb traç continu correspon al comportament amb la freqüència del model de la fig. 1, la qual es pot dividir en  4  trams ben diferenciats segons la freqüència de treball: 

            • A freqüències inferiors a   ω₁   la    r   s'ha de tenir en compte ja que el seu valor és important en front els valors que pren   ωL.

            • Entre   ω₁   i   ω₂ ,  a efectes pràctics es pot considerar la bobina com una inductància ideal, ja que   ωL >> r .

            • Entre   ω₂   i   ω_a   la proximitat de la freqüència d'auto-ressonància   ω_a   fa que s'hagi de tenir en compte la capacitat paràsita  c .

            • A freqüències superiors a   ω_a   la inductància queda totalment desvirtuada ja que es comporta com un condensador.

            Llavors, el primer que s'ha de conèixer abans d'utilitzar una inductància és la seva freqüència d'auto-ressonància     f_a = ω_a / 2π    ja que aquesta ens dirà la seva freqüència màxima d'utilització, i que s'ha de treballar bastant per sota d'aquesta freqüència per a que es comporti com una inductància.

            Com que normalment a la (3) es compleix    1/Lc >> (r/L)² ,  aquesta es pot simplificar i, a efectes pràctics,  tindrem:

expressió a partir de la qual podem conèixer la capacitat paràsita  c :    c = 1/ω_aL   (6)   un cop determinat el valor real de   L .

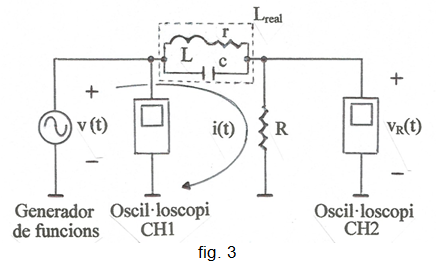
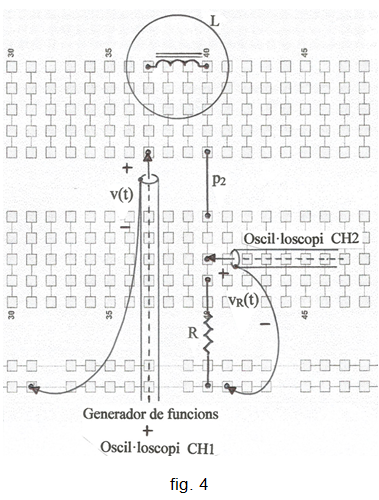
            Per determinar el valor real de   L   es pot emprar el mateix procediment de la pràctica:   Condensadors.  A la fig. 3 s'indica l'esquemàtic.

          Igual que a l'anterior pràctica : Condensadors , s'haurà de verificar que la magnitud de la impedància paràsita   Z_par  que introdueix l'oscil·loscopi i el cable coaxial sigui molt més gran que   R   per a que no falsegi els resultats -raoneu-ho.

          Relació de components:

 

 

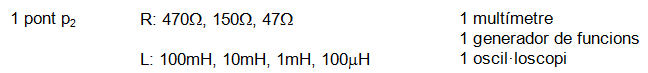
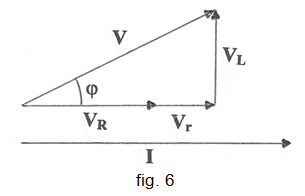
           El diagrama fasorial del circuit de la fig. 3, a freqüències compreses entre   0   i  ω₂   on es pot menystenir l'efecte de la capacitat paràsita   c , s'indica a la fig. 6.

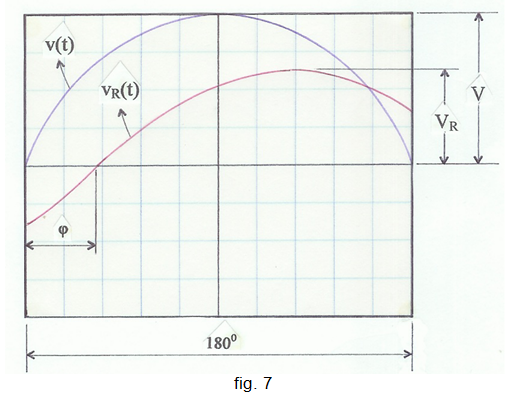
            A la fig. 7 s'indica com ajustar l'oscil·loscopi per obtenir la màxima resolució per mesurar l'angle de retard   φ   del corrent    i(t) = v_R(t)/R    respecte de la tensió aplicada  v(t) . 

Un cop escollit el valor de   R   cal ajustar el valor de la freqüència   f   de manera que el desfasament   φ  sigui de  45^o  amb la qual cosa es complirà    V_R + V_r = V_L , és adir:

i separant   L   d'aquesta expressió:   

      

Començant per la  L = 100 mH (nominal), seguim el següent procediment: 

             • Amb un multímetre mesurem la resistència   r   de la bobina.

             • Per determinar la   f_a  comencem fent un tanteig escollint   R = 470 Ω (nominal).  Amb forma d'ona sinusoïdal, el generador a màxima sortida i a màxima sensibilitat del  CH2, anem augmentant la freqüència fins que el corrent    i(t) = v_R(t)/R   passa per un mínim i està en fase amb  v_i(t).  Com que   v_i(t)   mai és perfectament sinusoïdal,  s'observarà  que  a  la forma d'ona del corrent a aquesta freqüència hi són presents harmònics   amb  més  o  menys  grau.  La  freqüència  a  la  qual  això ocorre serà   f_a   que val, per exemple : f_a = 125 kHz.

              • Cal ara comprovar si en aquesta determinació de  f_a  es compleix   Z_par >> R , per la qual cosa procedim igual que en la anterior pràctica : Condensadors :

que compleix la condició destjada. Com que la resistència d'entrada de l'oscil·loscopi    R_par = 1 MΩ >> 470 Ω   també compleix la condició, podrem donar per vàlid el valor obtingut per a   f_a , i continuem.  

             • Extreieu la resistència   R   del circuit, mesureu el seu valor real amb el multímetre i torneu-la a inserir en el circuit.  A l'oscil·loscopi tingueu cura que els canals estiguin en alterna, que posant-los a terra (GD) els traços apareguin ben centrats i, si cal, reajusteu la rotació del traç per a que aquests estiguin ben horitzontals.

             • Per    determinar    el    valor    real    de     L     es   va  disminuint  la  freqüència  fins  que el retard   φ   de   v_R(t) = Ri(t)   respecte de   v(t)   sigui de  45^o . Per aconseguir visualitzar aquesta situació es requereix molta cura i paciència.  A l'oscil·loscopi manipuleu la base de temps, el trigger mode i la  X-position  a la vegada que al generador de funcions es reajusten l'amplitud i la freqüència del senyal, fins aconseguir a la pantalla una imatge dels senyals tal com  s'indica  a  la   fig. 7, on  es  pugui veure, amb la màxima resolució que permet  l'oscil·loscopi,  que  la  tensió    v_R(t) = Ri(t)    està retardada  45^o  respecte de la tensió aplicada  v(t) .

             • Amb el valor de la freqüència finalment ajustada i el valor mesurat de  R , apliqueu  (7)  per trobar el valor real de  L.

              • Conegut el valor real de  L , apliqueu  (6)  per conèixer el valor de la capacitat paràsita  c. 

            Seguint el mateix procediment continueu amb la inductància de valor nominal 10 mH. Per a aquesta inductància empreu una   R   de  150 Ω   de valor nominal.

             Seguint el mateix procediment continueu amb les inductàncies de  1 mH  i  100 μH.  S'observarà que a mida que els valors d'inductància a determinar van variant caldrà anar variant també els valors de  R  a la fi d'aconseguir una freqüència adient per poder mesurar el desfasament de  45^o .

             Es suggereix mesurar els valor reals d'altres inductàncies de valors intermedis als emprats i, fins i tot, inferiors a  100 μH. Raonaeu la fiabilitat i les limitacions del mètode per a inductàncies molt petites.

            Observació:  en les inductàncies amb nucli ferromagnètic, les pèrdues en el nucli apareixeran incloses  en la resistència   r , amb la qual cosa aquesta resistència passarà a ser la resistència equivalent en sèrie de totes les pèrdues de la inductància. Les pèrdues en el conductor augmenten amb la freqüència degut a l'efecte pelicular i les pèrdues en el nucli augmenten també amb la freqüència, factors que contribueixen a augmentar el valor de   r  amb la freqüència.