El següent és un recordatori del concepte d'ona.
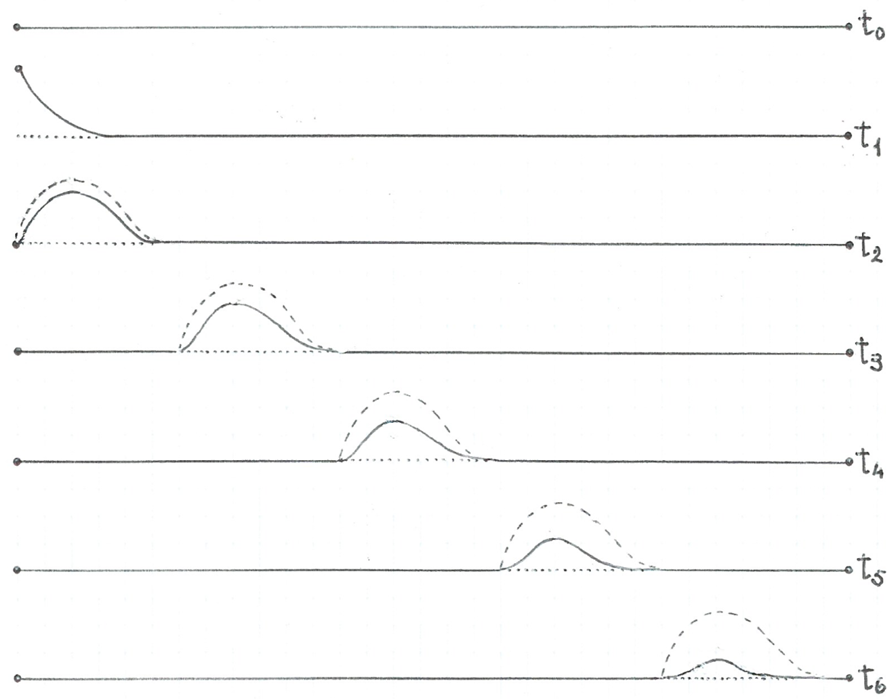
La fig.1 representa una corda estirada al terra, que en l'instant de temps t0 es troba en repòs.
fig. 1
Si durant un interval de temps t2 - t0 aixequem bruscament l'extrem esquerra de la corda i el tornem a deixar al terra, es produirà una pertorbació que es propagarà al llarg de la corda i que s'anirà atenuant a mida que aquella avanci. A una pertorbació que es propaga n'hi diem ona.
Les línies amb traç discontinu representen el cas ideal d'una corda perfectament elàstica, és a dir, sense pèrdues d'energia, on l'amplitud de la pertorbació es mantindria constant al llarg de la corda. Continuant amb aquesta situació ideal, quan la pertorbació arribés a l'extrem dret de la corda i en ell no es dissipés aquesta energia, s'aixecaria aquest extrem, tornaria a caure al terra i es produiria una nova pertorbació que es propagaria en sentit contrari -raoneu-ho. Com que en aquest cas ideal no hi hauria pèrdues d'energia, la pertorbació arribaria a l'extrem esquerra i el fenomen s'aniria repetint indefinidament.
A la pertorbació excitadora, que es propaga d'esquerra a dreta, n'hi diem ona progressiva i la que es propaga en sentit contrari, ona regressiva. En una corda real, és a dir, amb pèrdues d'energia, la pertorbació acabarà extingint-se i la corda recuperarà l'estat inicial de repòs que tenia abans de la pertorbació.
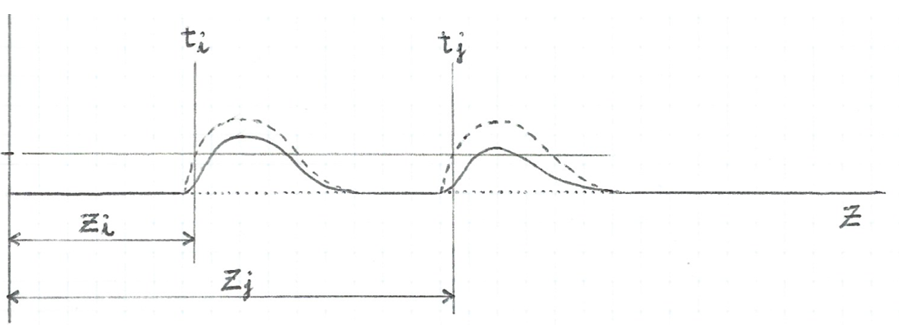
A la fig.2 es representa la corda damunt d'un eix d'abscisses z i en ordenades, l'amplitud de la pertorbació. Es representa també una pertorbació progressiva en dos instants de temps.
fig. 2
Si ti i tj , amb tj posterior ti , són dos instants de temps que corresponen a la mateixa fase de la pertorbació i zj - zi és la distància que separa aquestes dues fases iguals, llavors la velocitat de propagació vp de la pertorbació valdrà :

• Cal dir que aquesta anàlisi correspon al cas més senzill d'ones en una dimensió.
• Cal tenir present que tot el què s'ha exposat correspon a la situació ideal d'ones propagant-se en un medi sense pèrdues d'energia.