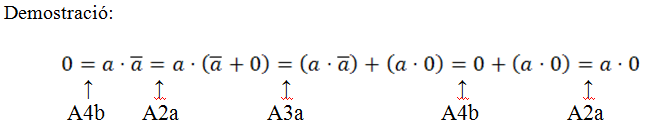El matemàtic anglès George Boole (1815-1857) va aplicar a la lògica una àlgebra que du el seu nom: àlgebra de Boole. El matemàtic nord-americà Edward Huntington (1874-1952) va establir els axiomes d'aquesta àlgebra i l'enginyer i matemàtic nord-americà Claude Shannon (1916-2001) va demostrar que les operacions booleanes elementals es podien representar mitjançant circuits de commutació senzills i que combinant aquests circuits es podien representar operacions més complexes. També va demostrar que l'àlgebra de Boole es útil per simplificar circuits de commutació. Per altra banda, a Shannon també se'l considera el pare de la Teoria de la Informació.
L'àlgebra de Boole treballa amb variables binàries, és a dir, variables que només poden prendre dos valors diferents, per exemple:
cert, fals encès, apagat alt, baix si, no obert, tancat activat, desactivat etc.
i tots aquests valors binaris es poden simbolitzar més breument assignant un 1 a un d'ells i un 0 a l'altre, llavors diem que es tracten d'un 1 i d'un 0 lògics i no s'han de confondre amb valors aritmètics. L'àlgebra de Boole, doncs, opera sobre conjunts de dos elements: {0, 1} .
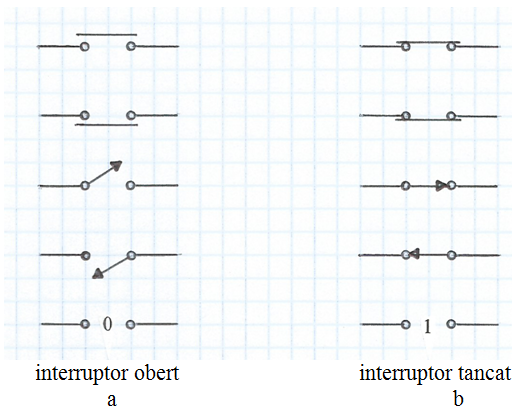
Els circuits elèctrics que accionen càrregues des de diferents punts utilitzen commutadors. El dispositiu de commutació més simple és l'interruptor. A les fig. 1a i 1b s'indiquen diverses representacions emprades per a aquest dispositiu el qual, a conseqüència de a la seva construcció, només pot romandre en una de les dues posicions: obert o tancat. Òbviament, aquesta àlgebra no té en consideració els fenòmens transitoris que es produeixen en les commutacions.
fig. 1
Les últimes representacions emprades a la fig. 1 avaluen la posició de l'interruptor mitjançant els símbols 0 per a l'interruptor obert i 1 per a l'interruptor tancat. Això és, simplement, un conveni i res no impedeix adoptar el conveni contrari, és a dir, el 0 per a l'interruptor tancat i l' 1 per a l'interruptor obert. Això no obstant, és més intuïtiu el conveni emprat a la figura i, en general, s'emprarà aquest. Així, l'àlgebra de la commutació és una àlgebra de Boole.
A la fig. 2 s'indica un interruptor on la seva posició ve donada pel valor de la variable a . Amb el conveni de la fig. 1, a = 0 significa interruptor obert i a = 1 interruptor tancat. Així, a és una variable independent ja que l'interruptor s'acciona a voluntat en el moment que es desitja.
fig. 2
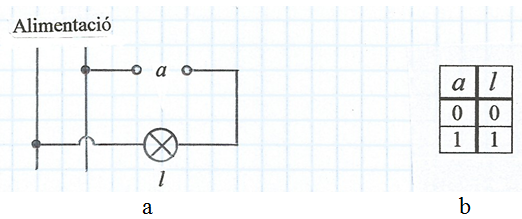
De la mateixa manera, quan una càrrega l està activada -bombeta encesa, motor en marxa, etc- podem assignar-li el valor l = 1 i quan està desactivada -bombeta apagada, motor parat, etc- el valor l = 0 . A la fig. 3a s'indica una bombeta -càrrega l - connectada a una línia d'alimentació a través d'un interruptor a . Així, l és una variable dependent o funció de a . A la fig. 3b s'indica una taula, denominada taula de la veritat, on es sintetitza el funcionament del circuit, en la qual s'indiquen les possibles situacions o valors de la funció l = a . En aquest cas tan senzill només hi ha una variable independent i la taula només té dues files i dues columnes.
fig. 3
Un axioma és una proposició que es considera evident i s'accepta sense demostració. Un teorema és una proposició demostrable a partir d'axiomes previs. L'àlgebra de Boole té els seus axiomes i teoremes i una manera de comprovar l'evidència d'aquests axiomes és emprant circuits de commutació i taules de la veritat.
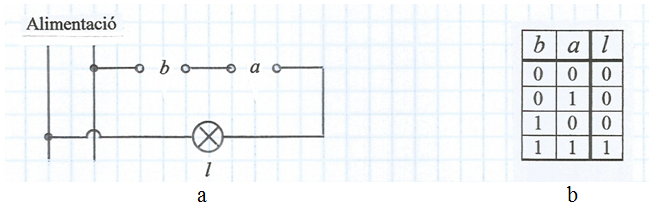
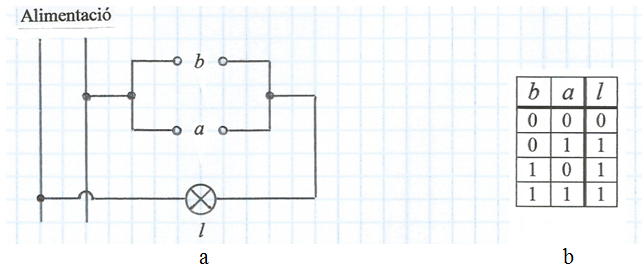
A la fig. 4a la bombeta l es connecta a la línia d'alimentació a través de dos interruptors a i b en sèrie. A la taula de la veritat de la fig. 4b s'indica l'evidència que la bombeta només estarà encesa (l = 1) quan ambdós interruptors estiguin tancats (a = 1 and b = 1). Es diu que el circuit representa l'operació lògica AND i també que la funció representa el producte lògic l = a · b , o més breument l = ab , degut a l'analogia dels valors de la taula amb el producte aritmètic:
0·0 = 0
0·1 = 0
1·0 = 0
1·1 = 1
No s'ha de confondre, però, el producte lògic, que és el resultat de combinar dues posicions, amb el producte aritmètic que és el resultat de multiplicar dos valors numèrics.
Com que ara hi ha dues variables independents el nombre de situacions possible s'ha duplicat -per a cada posició d'un dels interruptors n'hi poden haver dues per a l'altre interruptor- i la taula té ara tres columnes i quatre files.
fig. 4
És evident que si es permuten les posicions dels interruptors el circuit funciona exactament igual, d'on es desprèn un dels axiomes de l'àlgebra de Boole:
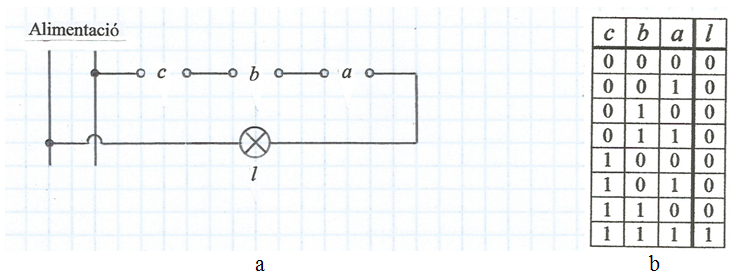
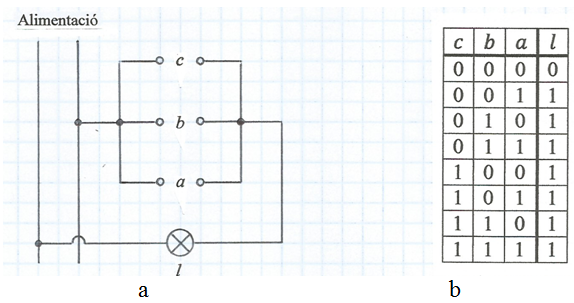
A la fig. 5a la bombeta l es connecta a la línia d'alimentació a través de 3 interruptors en sèrie. La taula de veritat de la fig. 5b indica la obvietat que la bombeta només estarà encesa quan els tres interruptors estiguin tancats. Com que ara hi ha una tercera variable independent el nombre de files de la taula es duplica passant a 8 files i el nombre de columnes a 4. El nombre de files d'una taula de la veritat correspon al nombre de variacions amb repetició de 2 elements -el 0 i l'1- presos de n en n essent n el nombre de variables independents. Així, per a n = 1: VR2,1 = 21 = 2; per a n = 2: VR2,2 = 22 = 4; per a n = 3: VR2,3 = 23 = 8 etc. Les diferents variacions s'ordenen tractant aquestes com si fossin nombres del sistema binari: de més petit a més gran. En altres casos és més convenient ordenar-les seguint el codi reflectit -o codi de Gray- on entre variacions consecutives només varia un dígit.
fig. 5
A la fig. 6a la bombeta l es connecta a la línia d'alimentació a través de dos interruptors a i b en paral·lel. A la taula de la veritat de la fig. 6b s'indica l'evidència que la bombeta estarà encesa (l = 1) quan al menys un dels interruptors estigui tancat (a = 1 or b = 1). Es diu que el circuit representa l'operació lògica OR i també que la funció representa la suma lògica l = a + b a la vista de la quasi analogia de la suma aritmètica amb els valors de la taula:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
on es posa de manifest aquesta quasi analogia ja que en la suma aritmètica 1 + 1 ≠ 1.
fig. 6
És evident que si es permuten les posicions dels interruptors el circuit funciona exactament igual, d'on es desprèn un altre dels axiomes de l'àlgebra de Boole:
A la fig. 7a la bombeta l està connectada a la línia d'alimentació a través de 3 interruptors en paral·lel. La taula de la veritat de la fig. 7b indica la obvietat que la bombeta estarà encesa quan al menys un dels interruptors estigui tancat.
fig. 7
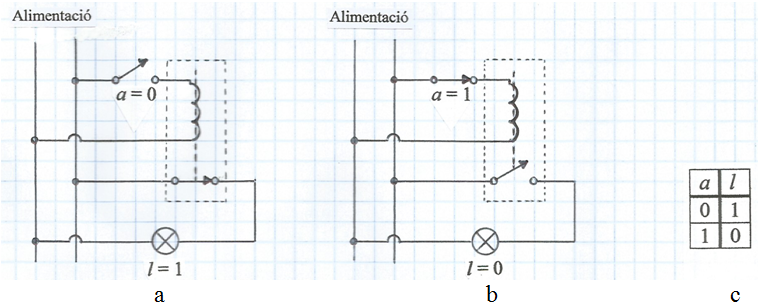
A la fig. 8 la bombeta està connectada a la xarxa d'alimentació a través d'un element intermedi: un relé. En aquest cas concret el relé disposa d'un interruptor que està tancat quan la bobina està desactivada (fig. 8a) i que s'obre quan aquella s'activa (fig. 8b). En aquestes condicions la bombeta estarà encesa (l = 1) quan l'interruptor a estigui obert (a = 0) i apagada (l = 0) quan a estigui tancat (a = 1). La taula de la veritat de la fig. 6c resumeix tot això. Es diu que aquest circuit fa la funció NOT , és adir, la inversa, complementaria o negada de la variable independent a i s'expressa com
fig. 8
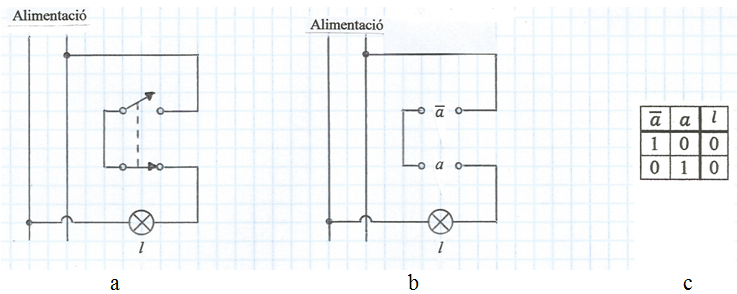
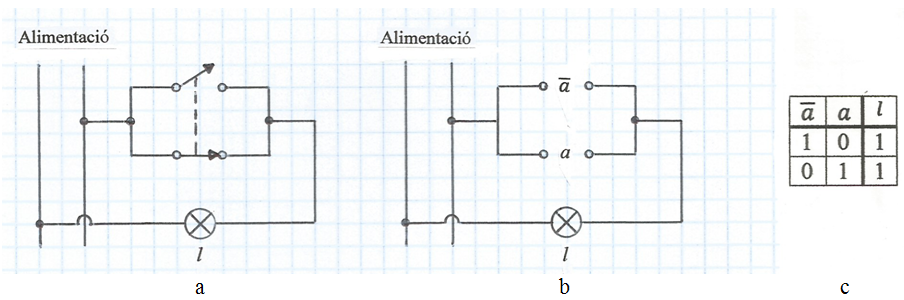
A la fig. 9a la bombeta l es connecta a la línia d'alimentació a través de dos interruptors en sèrie els mecanismes dels quals tenen una unió rígida indicada amb traç discontinu, de manera que quan un d'ells obre l'altre tanca, i viceversa. A la fig. 9b es representa el mateix circuit on s'indica com que la posició d'aquest interruptor és sempre la inversa, complementaria o negada de la posició a de l'altre interruptor. Com que els interruptors estan en sèrie estem davant d'un producte lògic i la taula de la veritat de la fig. 9c indica l'evidència que sempre l = 0 ja que sempre i haurà un interruptor obert.
fig. 9
Això ens porta a un altre axioma de l'àlgebra de Boole:
A la fig. 10a la bombeta l es connecta a la línea d'alimentació a través de dos interruptors en paral·lel els mecanismes dels quals tenen una unió rígida de manera que quan un d'ells obre l'altre tanca, i viceversa. A la fig. 10b es representa el mateix circuit on s'indica com que la posició d'aquest interruptor és sempre la inversa, complementaria o negada de la posició a de l'altre interruptor. Com que els interruptors estan en paral·lel estem davant d'una suma lògica i la taula de la veritat de la fig. 10c indica l'evidència que sempre l = 1 ja que sempre hi haurà un interruptor tancat.
fig. 10
Això ens porta a una altre axioma de l'àlgebra de Boole:
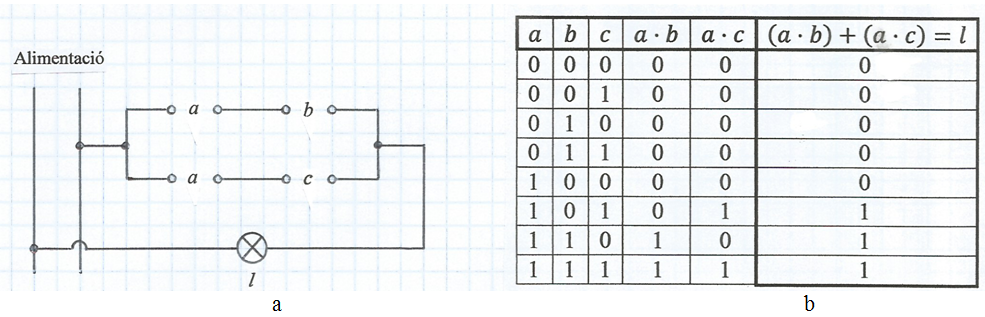
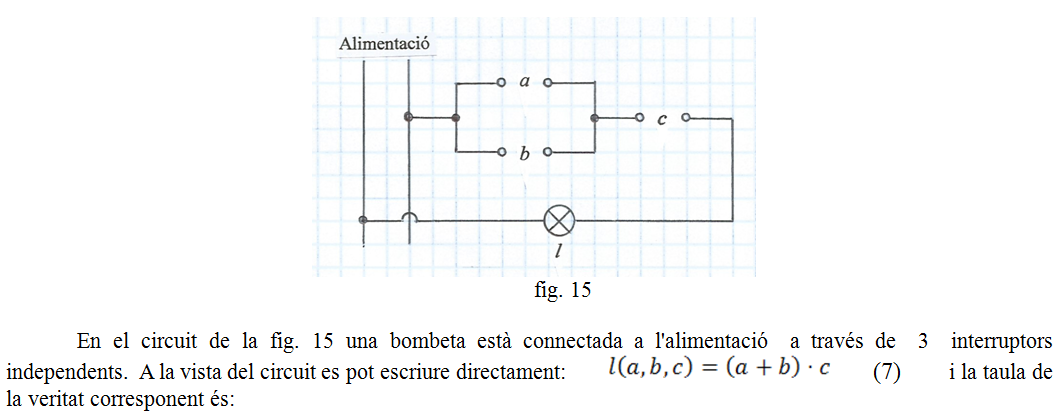
En el circuit de la fig. 11a es veu que els interruptors b i c són simples i l'interruptor a és doble, la qual cosa s'ha d'interpretar com que ambdós contactes obren i tanquen alhora degut a que els seus mecanismes tenen una unió rígida. A la vista del circuit podem expressar la funció que realitza: l = (a · b) + (a · c) . La taula de la veritat corresponent s'indica a la fig. 11b.
fig. 11
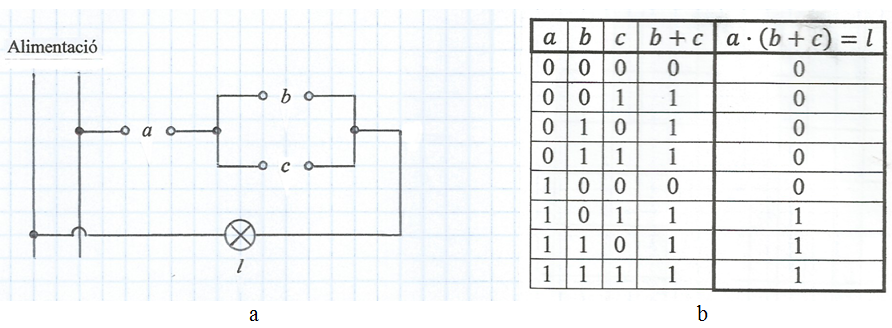
Observant el circuit resulta evident que l'interruptor doble a es pot substituir per un interruptor simple tal com s'indica a la fig. 12a. La funció que realitza aquest circuit és: l = a · (b + c) i la seva taula de la veritat s'indica a la fig. 12b. Comparant aquesta taula amb l'anterior es comprova dita evidència ja que els valors de l són idèntics.
fig. 12
L'anterior ens du a un altre axioma de l'àlgebra de Boole:
Observació: a l'haver adoptat els símbols · i + per al producte i suma lògics, respectivament, aquesta expressió coincideix amb l'expressió de la propietat distributiva del producte respecte a la suma de l'àlgebra ordinària.
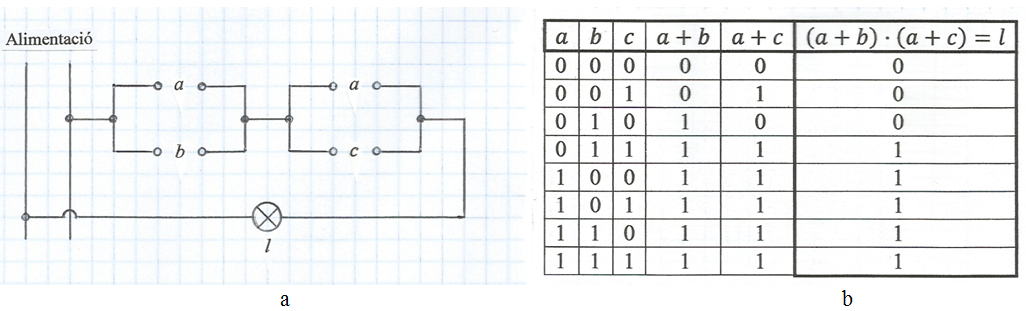
En el circuit de la fig. 13a, de nou els interruptors b i c són simples i l'interruptor a és doble amb la qual cosa ambdós contactes obren i tanquen alhora. A la vist a del circuit podem expressar la funció que realitza: l = (a + b) · (a + c) i la seva taula de la veritat s'indica a la fig. 13b.
fig. 13
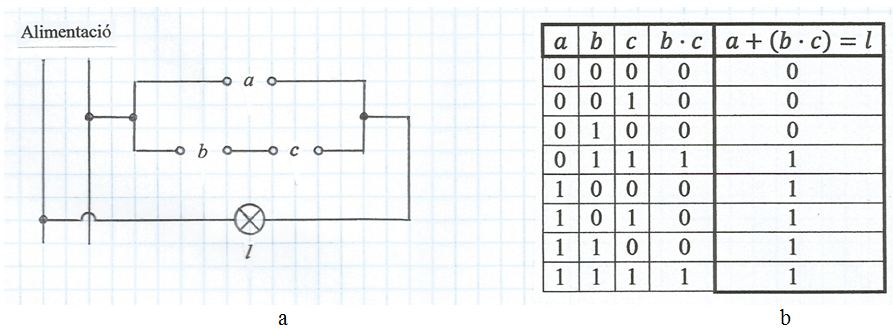
El circuit de la fig. 14a realitza la funció: l = a + (b · c) i a la fig. 14b s'indica la taula de la veritat corresponent.
fig. 14
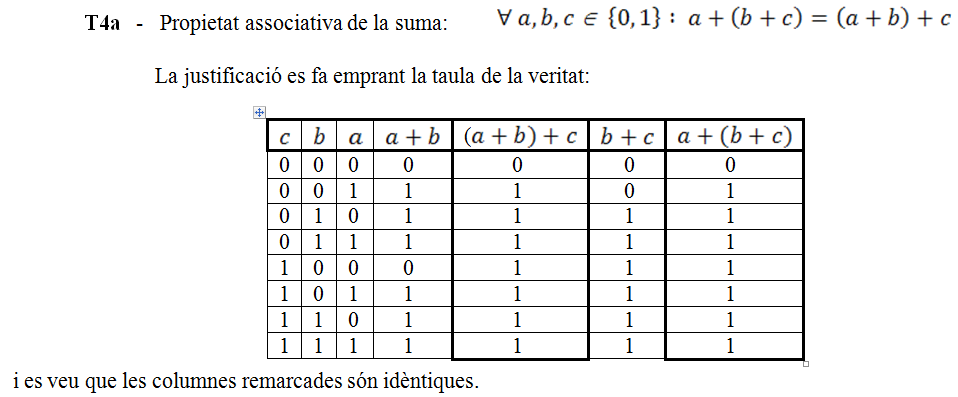
Comparant aquestes dues últimes taules es pot afirmar que aquests dos últims circuits realitzen la mateixa funció la qual cosa ens du a l'axioma que queda de l'àlgebra de Boole:
i s'observa que aquesta propietat no existeix a l'àlgebra ordinària.
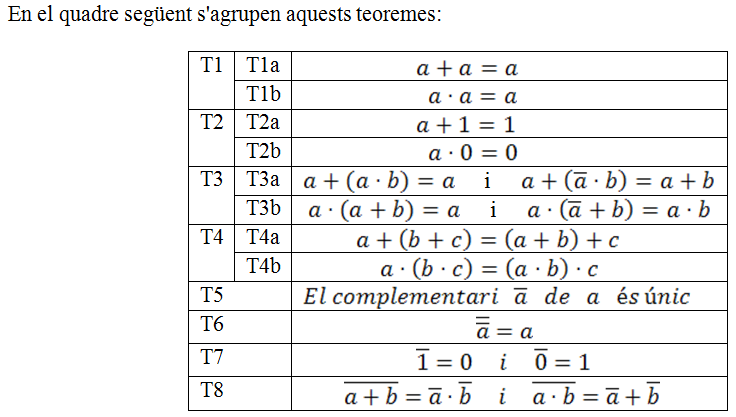
El compliment de tots aquests axiomes permet afirmar que el conjunt {0, 1} juntament amb les operacions de complementació, suma lògica i producte lògic és una àlgebra de Boole, la qual cosa es pot expressar més breument així: ({0, 1}, ¯ , + , · ) és una àlgebra de Boole. En el següent quadre s'agrupen aquests axiomes:
A partir d'aquests axiomes o mitjançant les taules de la veritat es poden demostrar els teoremes de l'àlgebra de Boole:

Les fórmules d'expansió de Shannon
Advertiment: per simplificar la notació, d'aquí en endavant es suprimiran parèntesi i es seguiran les mateixes prioritats d'operacions que en l'àlgebra ordinària.
i així successivament per a més de tres variables.
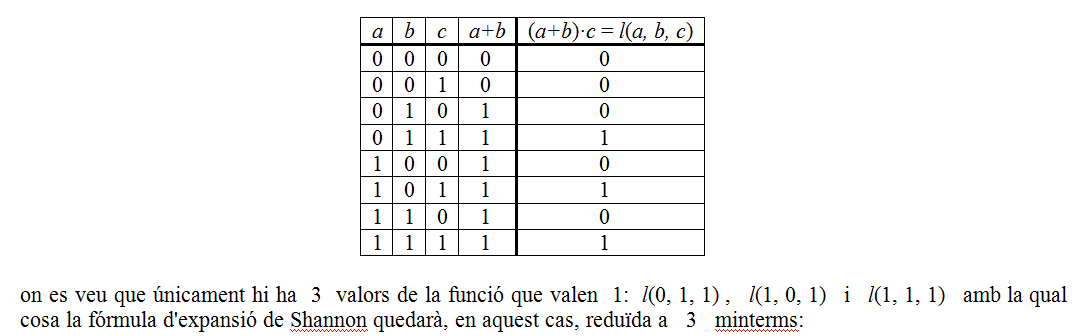
En aquesta 1a fórmula d'expansió de Shannon veiem que la funció f (a, b, c, · · ·) està expressada com una suma de productes i a cadascun d'aquests productes se'n hi diu minterm. En cada minterm apareixen totes les variables -negades o no-, llavors es diu que la funció esta expressada en forma canònica. Si n és el nombre de variables de la funció, el nombre màxim de minterms d'aquella serà 2n (raoneu-ho), ja que, depenent de la funció en particular, hi poden haver minterms nuls, aquells per als quals el valor de la funció valgui 0. Un exemple aclarirà tot això:
Commutadors
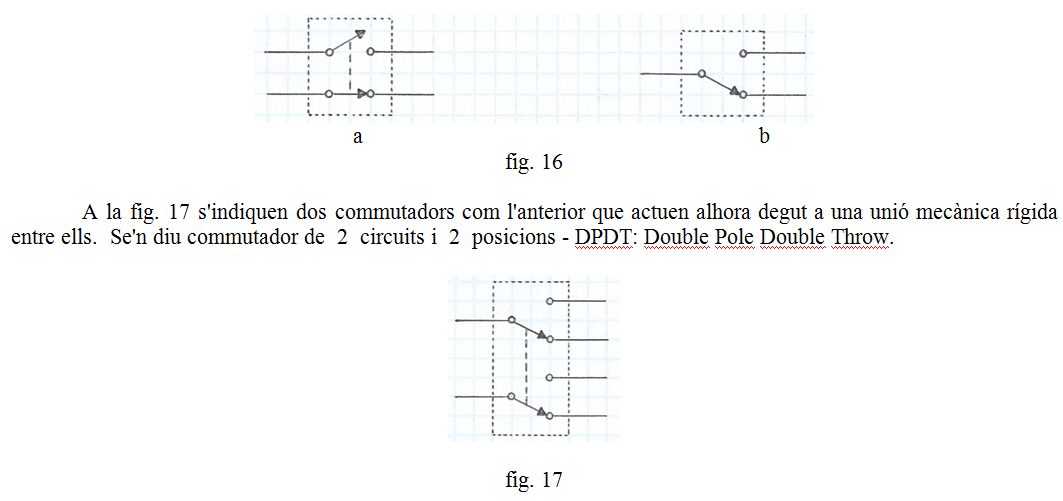
Els dos interruptors dels circuits de les fig. 9 i 10, que s'indiquen novament a la fig. 16a, tenen un total de 4 terminals. Aquests interruptors es poden construir unint internament els terminals dels contactes mòbils, amb la qual cosa resulta un dispositiu de 3 terminals (fig. 16b) que se'n diu commutador d' 1 circuit i 2 posicions -en la literatura tecnològica en llengua anglesa se'l denomina SPDT, inicials de Single Pole Double Throw.
Fe d'errates: Al principi del teorema T7 - Propietat del complement, on diu 1 = 0 , l'1 hauria d'estar negat.