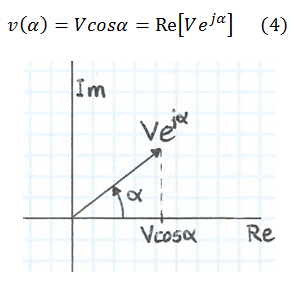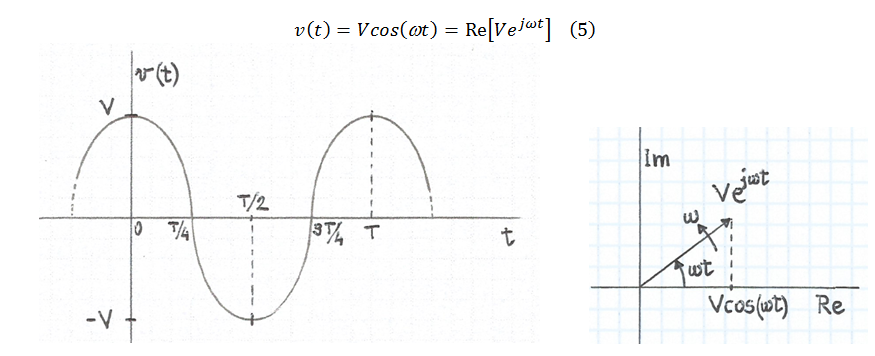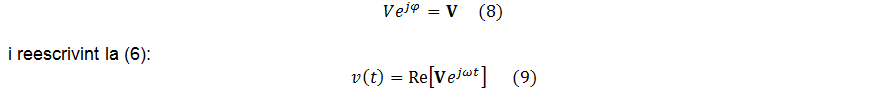L'anàlisi de circuits de corrent altern en el domini del temps on apareguin combinacions de resistències, inductàncies i capacitats, és feixuga, donat que s'han de resoldre equacions integro-diferencials.
En els circuits alimentats per una única font de tensió o corrent alterns, de freqüència f i treballant en règim permanent sinusoïdal -rps-, es avantatjós emprar nombres complexos per analitzar-los ja que faciliten els càlculs. Aquest mètode transforma les equacions integro-diferencials en el domini del temps, en equacions algebraiques en el domini de la freqüència. A més, proporciona una representació gràfica del funcionament del circuit molt més clara que no pas en el domini del temps.
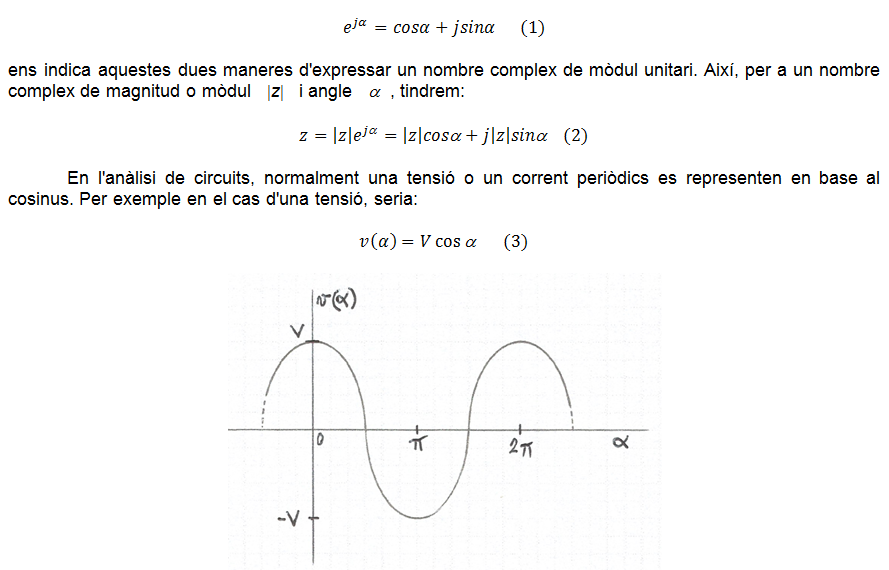
De les diverses formes d'expressar els nombres complexos, vistes a l'apèndix Introducció als Nombres Complexos, en el cas que ens ocupa ens interessen especialment les formes exponencial i trigonomètrica. La fórmula de Euler:
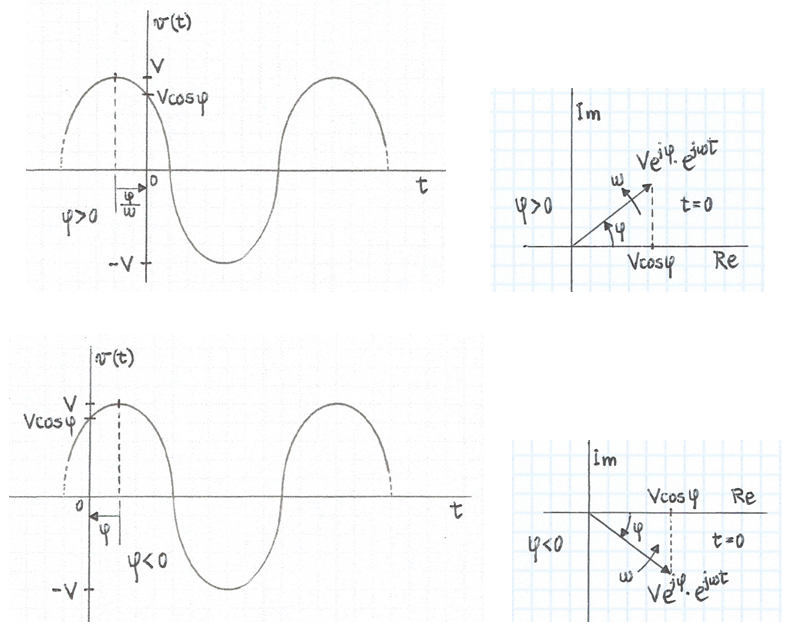
on V és l'amplitud o valor màxim o de pic de la tensió que, per definició, és un nombre real positiu i a un angle que fent-lo variar de 0 a 2π radians -o de 0 a 360o sexagesimals- la tensió pren tots els valors possibles al llarg d'un període T = 1 / f .
I ara el quid de la qüestió: comparant (3) i (2), es pot veure a v(a) com la part real del nombre complex , i ho expressem així:
Per obtenir una funció periòdica sinusoïdal en funció del temps, només cal expressar l'angle com una variable proporcional al temps: a = ωt on la constant de proporcionalitat ω és la velocitat angular -o també freqüència angular- a la que gira el complex: ω = 2π / T = 2πf . El sentit de gir es pren el positiu, és a dir, en sentit contrari al moviment de les busques d'un rellotge. Així, la (4) es transforma en la (5).
i la (7) ens diu que per a t = 0 , el complex forma un angle φ -angle o fase inicial- amb el semieix real positiu, i la seva projecció V cosα sobre l'eix ens dóna el valor de la tensió en aquest instant. Per simplificar la notació es fa:
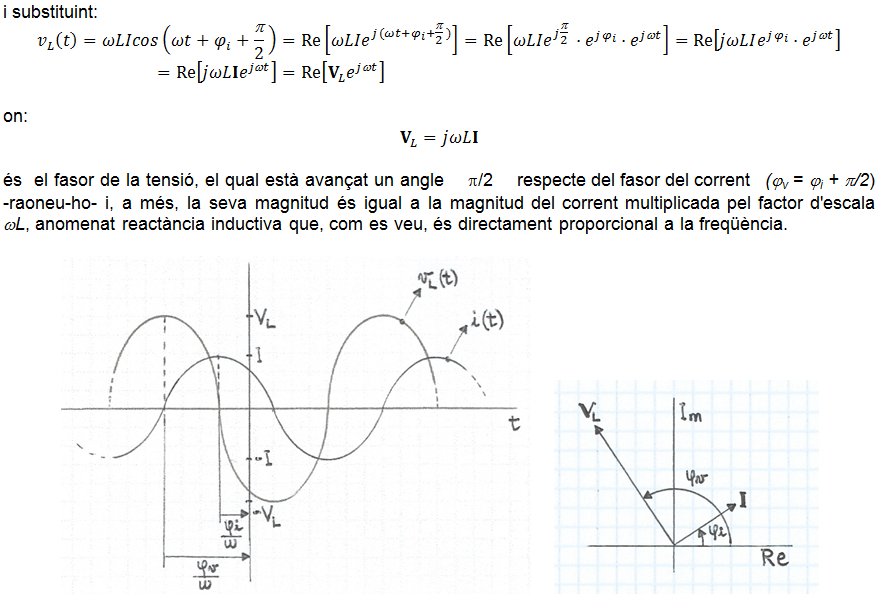
és el fasor de la tensió, el qual és igual al fasor del corrent multiplicat pel factor d'escala R , és a dir, ambdós fasors estan superposats o, el que és el mateix, estan en fase (φv = φi). El subíndex v de l'angle indica que correspon a la tensió.
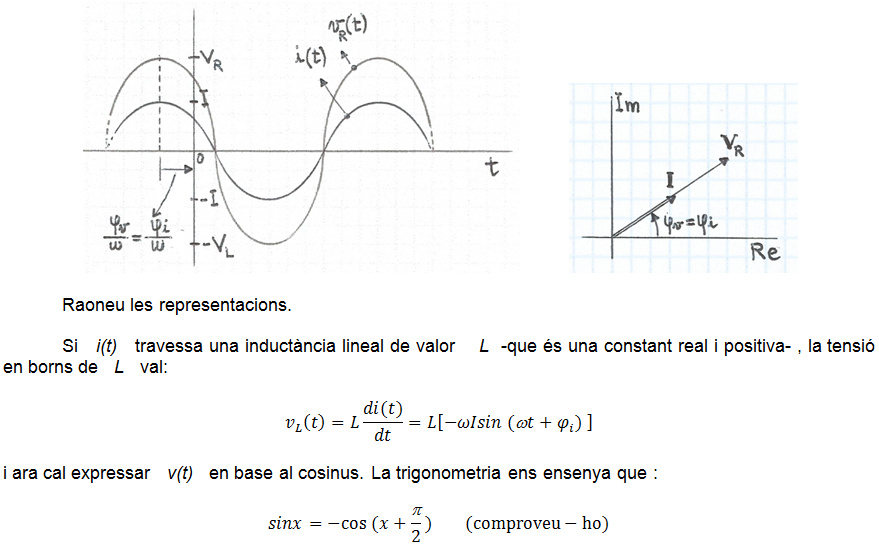
Raoneu les representacions.
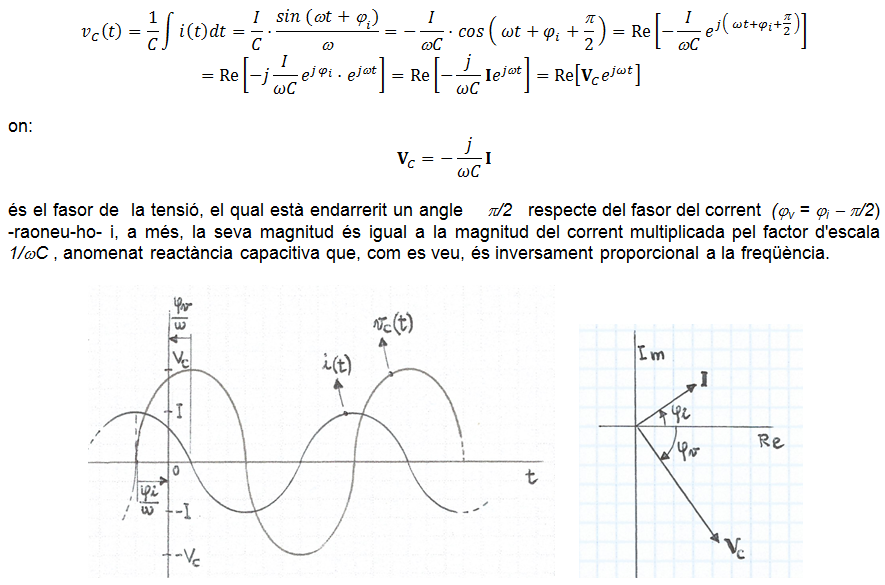
Si i(t) és el corrent de desplaçament en un condensador lineal de valor C -que és una constant real i positiva- , la tensió en borns de C val:
Raoneu les representacions
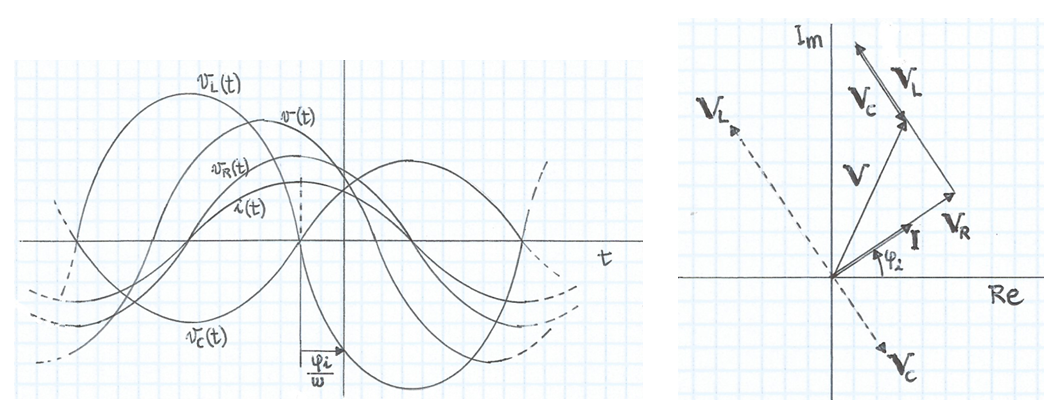
Amb un exemple es veuran els avantages d'emprar fasors. Aplicant la LKV al circuit de la figura:
A les figures s'ha representat el cas on la reactància inductiva predomina sobre la capacitiva: ωL >1/ωC , és a dir, VL >VC , amb la qual cosa l'avançament de V respecte de I està comprès entre 0 i 90o -raoneu-ho. Quan la reactància capacitiva predomina sobre la inductiva, és el retard de V respecte de I el que està comprès entre 0 i 90o -raoneu-ho. Si es compleix que ωL =1/ωC , ambdues reactàncies es cancel·len , V i I estan en fase i el circuit es comporta com si només hi hagués la resistència R -raoneu-ho. En aquest cas es diu que hi ha ressonància de tensions: VL = VC .
Suggeriment: analitzeu un circuit paral·lel RLC per comprovar que els fasors dels corrents compleixen la LKC. Igual que en el circuit sèrie, raoneu sobre les diferents situacions que es poden donar i sobre la ressonància de corrents.