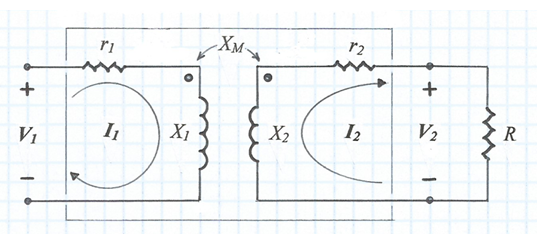
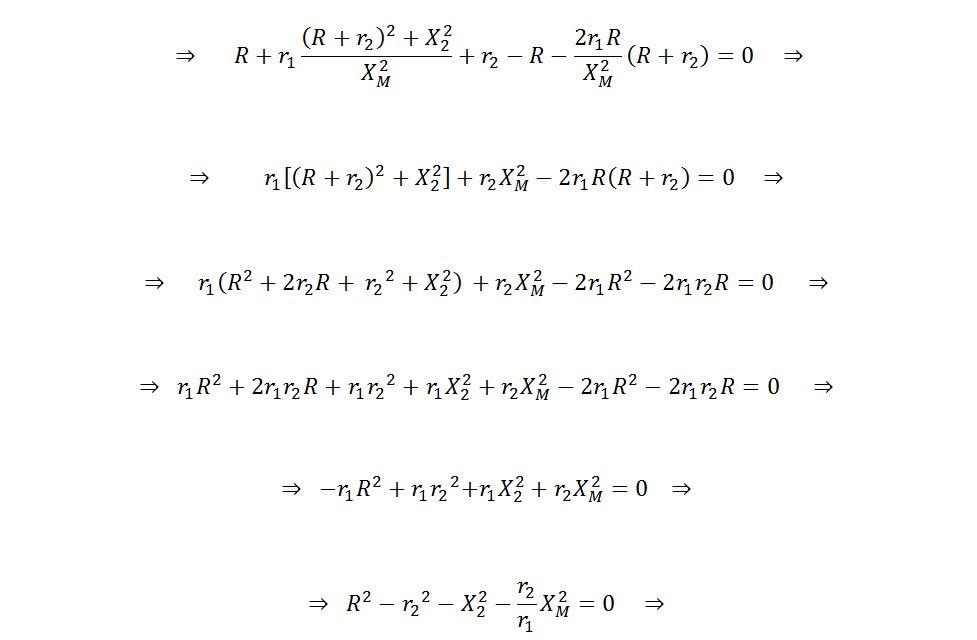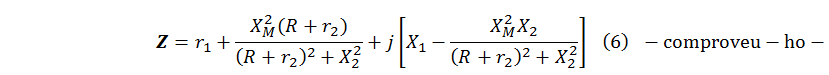A la fig. 1 s'indica l'esquemàtic d'un transformador funcionant en règim permanent sinusoïdal, el nucli del qual és aire. El debanat per on s'alimenta el transformador se'n diu primari i el debanat on es connecta la càrrega, secundari.

fig. 1

            V₁ , I₁ , V₂ , I₂   són els fasors corresponents a les tensions i els corrents, amb   V₁ , I₁ , V₂ , I₂   les amplituds o valors de pic respectius.

            r₁ , r₂   són les resistències dels debanats.

            X₁ , X₂  són les reactàncies dels debanats.

             és la reactància mútua, amb        la mitjana geomètrica dels coeficients d'acoblament .

            R   és la resistència de càrrega connectada al secundari.              

         El flux magnètic serà sinusoïdal per ser-ho la tensió aplicada al primari. Els corrents també seran sinusoïdals ja que la permeabilitat de l'aire és una constant (μ₀ = 4π·10^-7 Tm/A), d'aquí la denominació de transformador lineal -raoneu tot això.

           Les úniques pèrdues que presenta el transformador són per efecte Joule a les resistències dels debanats.

            Amb els sentits de referència adoptats, les LKV a cada costat del transformador ens diuen: 

expressió que correspon al circuit equivalent sèrie que "veu" la font.

             Com que   Z   és inductiva, si calgués compensar el factor de potència s'hauria d'intercalar en sèrie amb el primari un condensador la reactància del qual fos igual a la part imaginària de   Z   -raoneu-ho.  Per fer la compensació amb un condensador en paral·lel amb el primari s'hauria de trobar l'admitància    Y = 1 / Z   la qual ens donaria el circuit equivalent paral·lel, la part imaginària del qual ens permetria calcular el valor del condensador necessari -raoneu-ho.

i si, a més, l'acoblament fos perfecte (k = 1), la (14) seria:   que és un cas límit de transformador, abstracte, que n'hi diem transformador ideal.  Més endavant tornarem un mica sobre aquestes qüestions. Final del parèntesi. 

            El rendiment del transformador és:  η = P_R / P_t   amb   P_R  la potència útil, és a dir, la potència absorbida per la càrrega    R   i   P_t   la potència total absorbida pel conjunt transformador-càrrega, és a dir, la suma de la potencia útil i les pèrdues per efecte Joule en els debanats. Així, tindrem:

          Observació: la (21) ens diu que en el cas teòric d'un transformador sense pèrdues  ( r₁ = r₂ = 0 )  resulta   η_màx = 1 , com era d'esperar.  La indeterminació que apareix a la (20) en aquest cas, ens indica que aquest   100%   de rendiment s'aconseguiria per a qualsevol valor de   R  -raoneu-ho.

       Els següents raonaments ens conduiran a trobar un circuit equivalent per al transformador que ens ajudarà a entendre el seu funcionament.

            Si  el  transformador  no  tingués  pèrdues  i els debanats estiguessin perfectament acoblats  (k = 1), direm que el transformador és perfecte i les anteriors equacions (1) i (2) seran:

on   L₁ , L₂   són les inductàncies dels debanats,   N₁ , N₂   els nombres d'espires i a   n   se'n diu relació de transformació per a un transformador perfecte, i indica el nombre d'espires del primari per cadascuna del secundari -raoneu tot això. Observem que aquest resultat està d'acord amb la (9).

            Si   n > 1  diem que el transformador és reductor de tensió ja que la càrrega s'alimenta a una tensió   V₂ < V₁ . Si   n < 1  és elevador de tensió ja que serà   V₂ > V₁ . Així, mitjançant un transformador es pot alimentar una càrrega que requereix una tensió determinada, amb una font que proporciona una tensió diferent.            

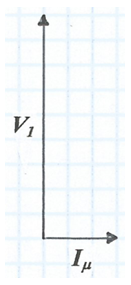
            Quan un transformador sense pèrdues està en buit -no hi ha cap càrrega connectada al secundari-, per a una determinada tensió  V₁  el corrent pel primari ve fixat només per la reactància  X₁  i se'n diu corrent magnetitzant    I_μ    que,  juntament  amb  el  nombre  d'espires    N₁ , és el que produeix el flux magnètic:   Ø  = N₁I_μ / ℜ    amb   Ø    l'amplitud del flux i   ℜ   la reluctància del nucli.  En aquestes condicions no s'absorbeix potencia activa ja que   V₁   i   I_μ   estan en quadratura (fig. 2) -raoneu-ho.

fig. 2

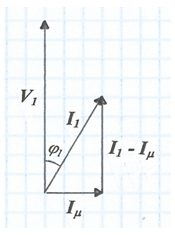
            Quan  es  carrega  el  secundari  amb  una  càrrega   R ,  la  potència   P_R   dissipada  per aquesta val:  P_R = RI_2ef²    i que, òbviament, l'ha de proporcionar la font; llavors, en el primari apareixerà un altre corrent en fase amb    V₁   que s'afegirà a    I_μ    (fig. 3) de manera que el corrent resultant    I₁   formarà un angle   φ₁ < 90^o   amb   V₁   i la potència activa     V_1ef  I_1ef  cosφ₁    serà igual a   P_R   -raoneu tot això.

fig. 3

              Si s'augmenten el nombre d'espires   N₁  i  N₂   mantenint però la relació de transformació   n = N₁/N₂  , el valor de   I_μ  es reduirà proporcionalment -raoneu-ho.

             I ara fem una abstracció: si mantenint la   n   fem tendir   N₁  i   N₂    a infinit, llavors   I_μ    tendirà a zero, la qual cosa vol dir que pel primari només hi haurà corrent quan es carregui el secundari.  Com que en aquestes condicions   I₁  estarà en fase amb   V₁  -raoneu-ho- es complirà:  

P_R = RI_2ef² = V_2ef  I_2ef  = V_1ef I_1ef     (25)

és a dir:

I₂ / I₁ =  V₁ / V₂ = n     (26)

              A aquest model abstracte de transformador n'hi diem transformador ideal, on es compleix no només  V₁ / V₂ = n   -condició de transformador perfecte- sinó que, a més,   I₂ / I₁ = n   -condició de transformador ideal. 

            Com que en un model ideal   V₁   i   I₁   estan en fase això vol dir que la font "veu" una càrrega resistiva equivalent a    Z = V₁ / I₁  (27).  Si a la (27) posem   V₁   i   I₁   en funció de   V₂   i   I₂   i de la relació de transformació   n , tenim:

Z = nV₂ / (I₂/n)  =  n²(V₂/I₂)  = n²R     (28) 

i  la  (28)  ens  diu  que  la  font  "veu"  una  resistència  reflectida al primari   n²   vegades la   R .  Observem que aquest resultat és l'obtingut a la (15).

            Si   n >1  -transformador reductor de tensió-  la   resistència   reflectida   serà     n²     vegades   superior   a    R    i   si     n < 1   -transformador elevador de tensió- ,  n²   vegades inferior.

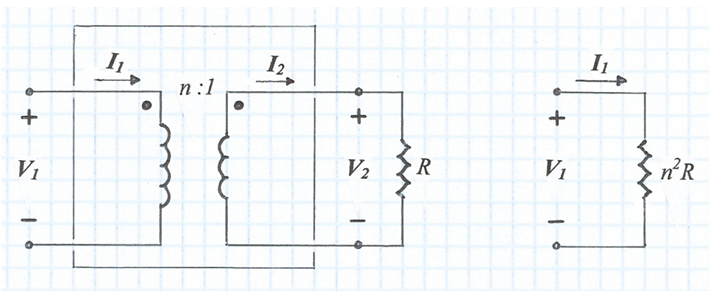
            A la fig. 4a es representa aquest model carregat amb la   R   i a la fig. 4b, la càrrega reflectida que "veu" la font.

            fig. 4a                                                             fig. 4b

            Així, en els casos on cal obtenir la màxima potència que pot proporcionar una font, es pot utilitzar un transformador per adaptar -igualar- el valor d'una càrrega al valor de la seva resistència interna. Un transformador ideal seria un adaptador d'impedàncies ideal.

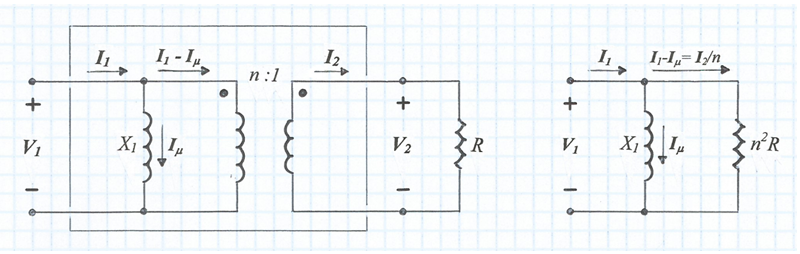
            El model de transformador perfecte es pot representar a partir de l'ideal afegint-li la reactància finita X₁   en paral·lel amb el primari, tal com s'indica a la fig. 5a -raoneu-ho.  A la fig. 5b es representa el circuit equivalent que "veu" la font.

                 fig. 5a                                                                           fig. 5b

            El circuit equivalent de la fig. 5b indica que la font "veu" una càrrega inductiva. Si calgués compensar aquesta component inductiva només s'hauria d'afegir un condensador en paral·lel, la reactància del qual fos del mateix valor   X₁ -raoneu-ho.

            En el cas més real de   k < 1  -però encara un transformador sense pèrdues: r₁ = r₂ = 0- les equacions (1) i (2) serien:

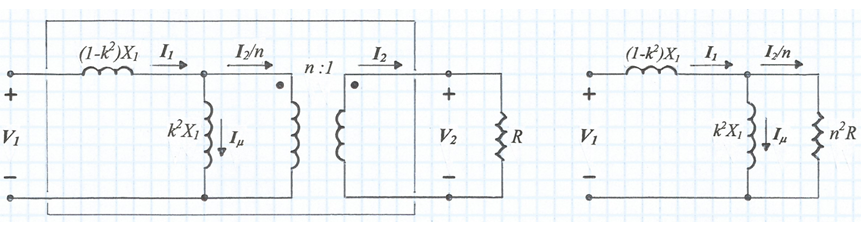
i la (32) ens diu el següent:  (1-k²)X₁  significa la part de la reactància que produeix la dispersió de flux -reactància  de dispersió- i    k²X₁   la part útil, és a dir, la part que s'acobla perfectament -observem que   k²X₁ / X₂ = n².  El corrent    I₂ /n   suggereix emprar un transformador ideal en paral·lel amb   k²X₁ , com indica la fig. 6a -raoneu-ho.  A la fig. 6b s'indica el circuit equivalent -raoneu.  

                 fig. 6a                                                                                         fig. 6b

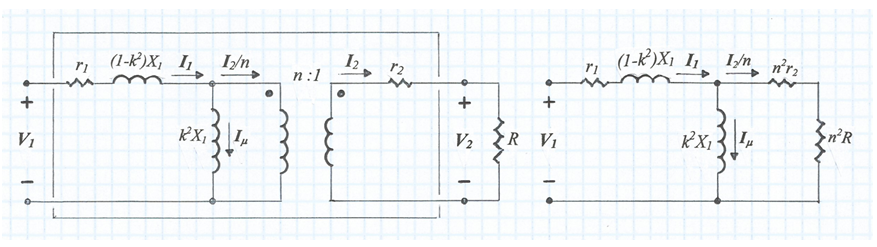
            Ara només resta tenir en compte les resistències dels debanats per arribar al circuit equivalent real d'un transformador amb pèrdues, per la qual cosa només cal afegir aquestes resistències als circuits de les fig. 6a i 6b, tal com s'indica a les fig. 7a i 7b.

            fig. 7a                                                                            fig. 7b

            Observant el circuit equivalent de la fig. 7b, la impedància que "veu" la font d'alimentació val:

            Manipulant la (33) i fent les substitucions oportunes tenint en compte (8) i (9), es pot comprovar que coincideix amb la (6), com és d'esperar -es suggereix fer-ho com exercici.

Escriure un comentari