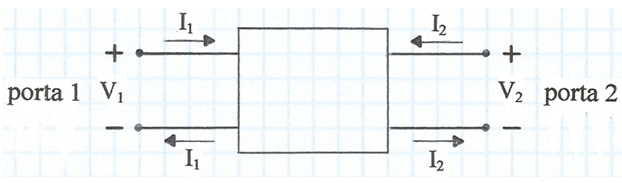
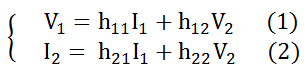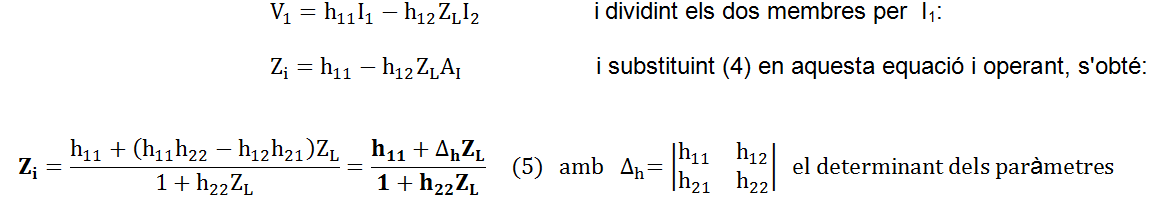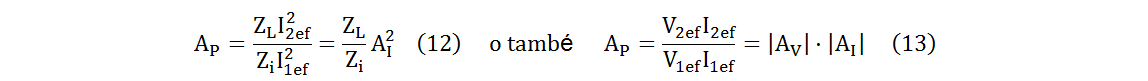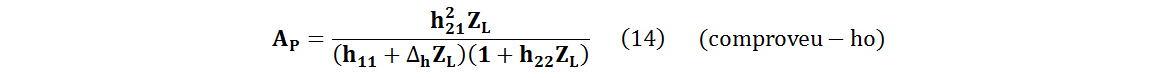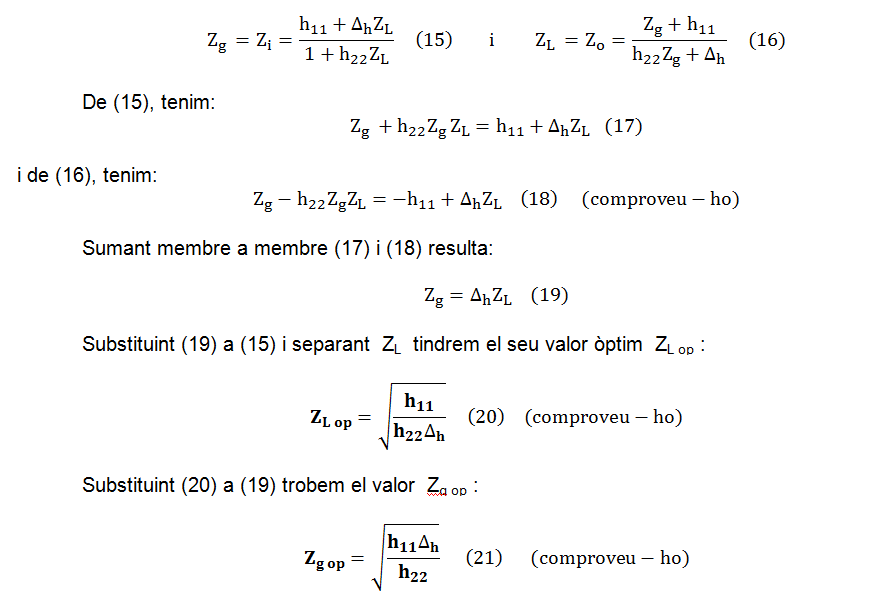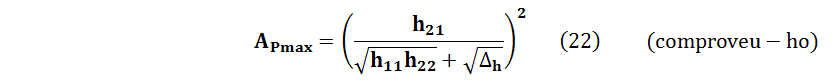Se'n diu quadripol a tota xarxa lineal, de topologia arbitrària, que no contingui fonts independents i que es pugui enquadrar dins d'una "caixa" de manera que aquesta tingui dues portes, és a dir, dos parells de terminals on en cada parell es compleixi que el corrent que entra per un terminal és igual al que surt per l'altre. A la fig. 1 es representa un quadripol amb els sentits de referència adoptats per als corrents i les tensions.
fig. 1
Un quadripol és un model potent que permet caracteritzar components o seccions de circuits -transistors, amplificadors, filtres, etc.- de manera que no cal descendir fins al nivell dels components interns a l'hora d'analitzar la xarxa. Expressant dues variables en funció de les altres dues, el quadripol queda totalment caracteritzat. Un quadripol proporciona un circuit equivalent senzill d'analitzar mitjançant un joc de quatre paràmetres que relacionen els corrents i les tensions de les portes. Aquestes quatre variables es poden combinar fins a 6 maneres diferents, el que dóna lloc a sis jocs de paràmetres. El joc de paràmetres híbrids -paràmetres h- molt utilitzats en electrònica, es defineixen amb el següent sistema d'equacions:
En aquest sistema es prenen I1 i V2 com variables independents i V1 i I2 com funcions.
En el domini de la freqüència complexa s , que és el cas més general, totes les variables i paràmetres dependran de s . En règim permanent sinusoïdal, les variables seran fasors i els paràmetres -impedàncies, admitàncies i adimensionals- seran nombres complexos. En corrent continu, les variables seran els valors de contínua de les tensions i els corrents, i els paràmetres seran resistències, conductàncies o adimensionals.
Considerant la porta 1 com l'entrada del quadripol i la porta 2 com la sortida, aquests paràmetres signifiquen:
• fent V2 = 0:
h11 = V1 / I1 és la impedància d'entrada amb la sortida curtcircuitada.
h21 = I2 / I1 és el guany de corrent directe amb la sortida curtcircuitada, que és
adimensional
• fent I1 = 0:
h12 = V1 / V2 és la transferència inversa de tensió amb l'entrada en circuit obert, que
és adimensional
h22 = I2 / V2 és l'admitància de sortida amb l'entrada en circuit obert.
Observant l'equació (1), veiem que V1 és la suma de dues tensions: la caiguda de tensió h11I1 provocat pel corrent I1 a través de la impedància h11 i una tensió h12V2 controlada per la tensió V2 .
Observant l'equació (2), veiem que I2 és la suma de dos corrents: un corrent h21I1 controlat pel corrent I1 i un corrent h22V2 provocat per la tensió V2 a través de l'admitància h22 .
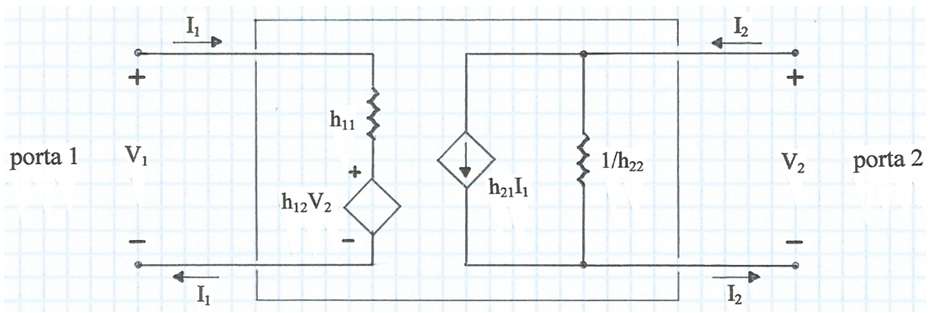
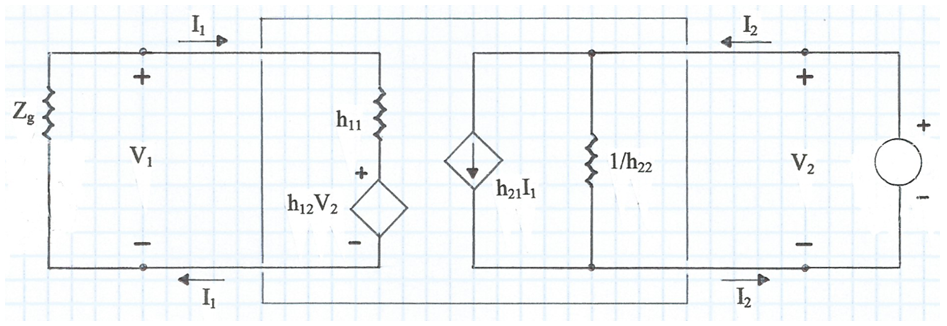
El sistema d'equacions anterior ens defineix, doncs, el circuit equivalent de la fig. 2 en l'interior del quadripol.
fig. 2
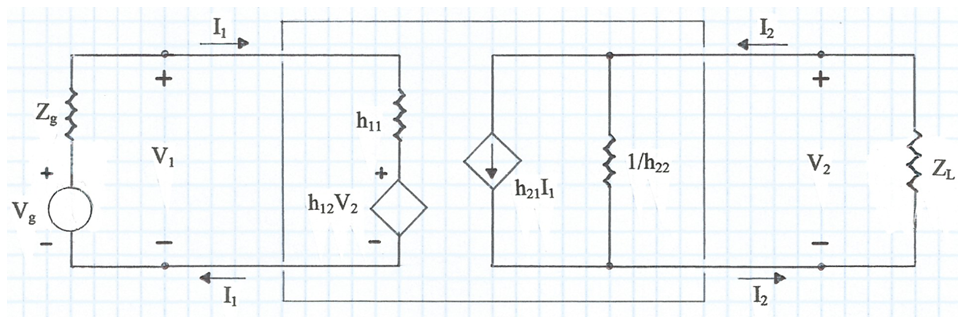
A la fig. 3 s'ha carregat la porta de sortida del quadripol amb una impedància ZL i s'alimenta per la porta d'entrada amb una font de tensió Vg i impedància interna Zg .
fig. 3
En aquestes condicions, V2 = -ZLI2 (3) i es defineixen les següents característiques del quadripol en funció dels paràmetres h i de ZL :
• Guany de corrent: AI = I2 / I1
Substituint la (3) a la (2) i separant el quocient I2 / I1 s'obté:
Si es fa ZL = ∞ -porta de sortida en circuit obert- el guany de corrent és zero, i si es fa ZL = 0 -porta de sortida en curtcircuit- el guany de corrent coincideix amb h21 .
• Impedància d'entrada: Zi = V1 / I1
Substituint la (3) a la (1):
(comproveu-ho). Si es fa ZL = ∞ -porta de sortida en circuit obert- la impedància d'entrada val Δh / h22 , i si es fa ZL = 0 -porta de sortida en curtcircuit- la impedància d'entrada coincideix amb h11 .
• Guany de tensió: AV = V2 / V1
Separant I2 de (3) i substituint-la a (2):

Si es fa ZL = ∞ -porta de sortida en circuit obert- el guany de tensió val -h21 / Δh . Si es fa ZL = 0 -porta de sortida en curtcircuit- el guany de tensió val zero.
Desactivant la font de l'entrada i alimentant el quadripol per la porta de sortida (fig. 4), es complirà V1 = -ZgI1 (9) .
fig. 4
Es defineix la:
• Impedància de sortida: Zo = V2 / I2
Substituint (9) a (1) i separant I1 resulta:
• Guany de potència: AP = P2 / P1
Es defineix el guany de potència AP com el quocient entre la potència P2 entregada a la càrrega i la potència P1 que entrega la font de l'entrada al conjunt quadripol-càrrega. Si la impedància de la càrrega ZL és resistiva i els paràmetres h són també resistius -amb la qual cosa la impedància d'entrada Zi també ho serà- el guany de potència valdrà:
Substituint (4) i (5) a (12), s'obté:
Si es substitueixen (4) i (8) a (13), s'arriba a la mateixa expressió (14) ,com és d'esperar, però el procediment és més laboriós (comproveu-ho).
És interessant trobar els valors resistius òptims per a Zg i ZL per a que AP sigui màxim. AP serà màxim quan hi hagi adaptació tant a l'entrada com a la sortida del quadripol, és a dir, quan es compleixi:
Substituint (20) a (14) i operant, trobem el guany de potència màxim:
En un quadripol que contingui elements actius, la potència d'entrada sol ser petita i és fàcil aconseguir l'adaptació en aquesta porta. A la porta de sortida no és tant senzill aconseguir l'adaptació ja que, possiblement, requeriria emprar un transformador adaptador d'impedàncies, la qual cosa representa un component voluminós, d'elevat cost i causa de distorsió.
Per aquest motiu, de vegades s'utilitza un altre guany: el guany de transferència APt , que és la relació entre la potència de sortida i la potència que proporcionaria la font de l'entrada si estigués connectada directament a una càrrega igual a la seva resistència interna. Aquest concepte és una útil figura de mèrit del quadripol per a unes condicions específiques de la font d'entrada i de la càrrega de sortida.
Si Vg és la tensió de la font i Zg la seva resistència interna, la màxima potència que aquesta pot proporcionar val: