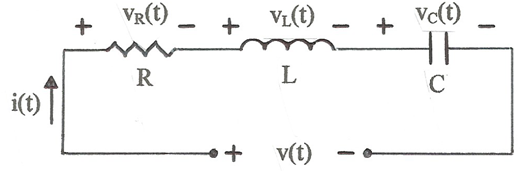
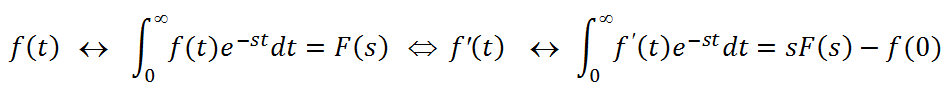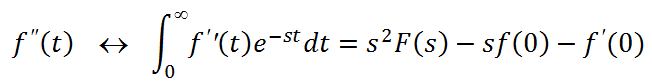En molts àmbits de l'enginyeria i de la ciència, ens trobem amb equacions diferencials i integro-diferencials lineals certament feixugues de resoldre pels mètodes tradicionals. Afortunadament el matemàtic Pierre-Simon de Laplace (1749-1827) ens va llegar un mètode expeditiu per resoldre aquestes equacions: la Transformada de Laplace (TL). Aquest mètode permet transformar les equacions diferencials lineals en equacions algebraiques, molt més fàcils de resoldre. Per exemple, aplicant la LKV al circuit de la fig. 1, tenim:
fig. 1
i derivant (1):
Suposant condicions inicial nul·les ( vC(0) = 0 i i(0) = 0 ), el mètode de Laplace -que s'explicarà de seguida- transforma la (2) així:
on es passa del domini del temps t en l'equació diferencial (2) al domini d'una variable s en l'equació polinòmica (3): v(t) es transforma a V(s) i i(t) a I(s). Les derivades de les funcions es transformen també a V(s) o I(s) i a més queden multiplicades per s elevada a un exponent igual a l'ordre de la derivada. Com que les arrels dels polinomis poden ser complexes, llavors la variable s serà en general complexa i, en conseqüència, V(s) i I(s) seran en general funcions complexes.
En l'anàlisi de circuits la TL s'utilitza per determinar els transitoris de corrents i tensions que es produeixen a partir de l'instant en que se'ls aplica una excitació o apareix una pertorbació -instant que es pren com zero- fins que el circuit arriba al seu règim estacionari o permanent. En els circuits estables els fenòmens transitoris es van extingint amb el temps, ja sigui asimptòticament o fluctuant cada cop menys al voltant d'un valor estacionari final, la qual cosa vol dir que teòricament duren eternament encara que a la pràctica es considera que passat un temps suficient, determinat per les constants del circuit, el transitori es pot considerar extingit. Per definir la TL, però, cal el rigor de considerar que els transitoris duren eternament per la qual cosa es té en compte el comportament d'aquests des de zero fins infinit, en conseqüència s'han de considerar també els senyals d'excitació durant tot el temps, és a dir, des de zero fins infinit.
Com veurem, la TL relaciona funcions del temps amb les àrees definides entre aquestes funcions i els eixos. Si una funció del temps f(t) -una tensió o un corrent- s'integra entre zero i infinit, pot ser que l'àrea entre la funció i els eixos sigui finita, amb la qual cosa la integral convergeix. Però podria ser que aquesta àrea no fos finita, amb la qual cosa la integral no convergeix; això passa, per exemple, amb els senyals d'excitació esglaó o rampa. Per forçar la convergència de la integral en qualsevol cas, abans d'integrar es multiplica f(t) per una altra funció g(t) , escollida estratègicament, de manera que la integral del producte f(t)·g(t) entre zero i infinit convergeixi. Òbviament el valor d'aquesta àrea finita dependrà, a més de f(t) , de g(t) .
La transformació de Laplace consisteix en el què s'acaba de dir: multiplica una funció del temps f(t) per una funció estratègica g(t), que se n'hi diu nucli de la transformació, la qual asseguri la convergència de la integral del producte f(t)g(t) entre zero i infinit. El nucli de la transformació que s'escull per a la TL és la funció exponencial
e-st on s és un paràmetre que, degudament acotat, assegura la convergència de la integral. A més, la TL aprofita una propietat que té la funció exponencial: tant la seva derivada com la seva integral són també exponencials.
En definitiva, si a una funció f(t) se li fa la següent operació de forma que la integral
convergeixi, s'obtindrà un valor que només dependrà del paràmetre s ja que a l'integrar, la variable temps desapareix, és a dir, s'obtindrà una funció del paràmetre s , F(s) . Resulta així, una correspondència biunívoca entre f(t) i l'àrea F(s):
La (4) és la definició de la TL d'una f(t). La transformada de Laplace inversa (TL-1) de F(s) serà f(t) .
Cal veure que el nucli de la transformació e-st és una funció que no té dimensions ja que l'únic que fa és amortir la funció f(t) la qual sí que tindrà dimensions -tensió, corrent,···. Com que e-st no té dimensions, les dimensions del paràmetre s han ser temps-1 -raoneu-ho. Les dimensions de F(s) seran les del producte f(t)·t -raoneu-ho.
Si es coneix la TL d'una funció f(t) llavors es pot trobar fàcilment la TL de les seves derivades, i aquesta és la principal propietat de la TL:
integral que es resol pel mètode d'integració per parts. Seguint pel mateix camí es troba:
i així les derivades successives. Suposant condicions inicials nul·les (f(0) = f'(0) = 0), les expressions anteriors justifiquen la transformació de l'equació diferencial anterior (2) a la algebraica (3).
Es tracte, doncs, de disposar d'una taula amb les f(t) més usuals i les seves transformades F(s) .
Un cop transformada l'equació diferencial es separa la F(s) -tensió V(s), corrent I(s), ···- i anant a la taula es localitza la transformada inversa f(t) corresponent -tensió v(t), corrent i(t) ···. En molts casos, però, no cal tornar al domini del temps ja que des del domini de s es pot obtenir tota la informació sobre el funcionament del circuit. El domini de s ens dóna una altra visió, una altra manera d'interpretar el comportament dels circuits, i dels sistemes en general.