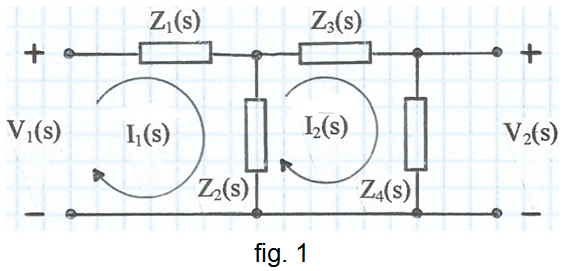
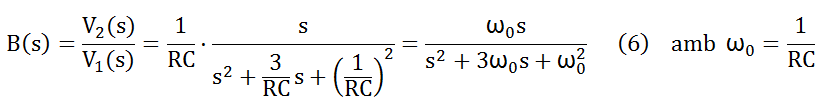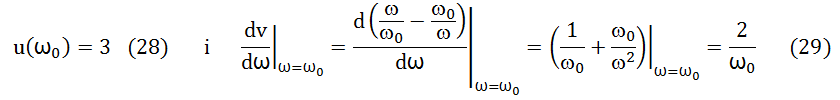La topologia de la xarxa de la fig. 1 és pot utilitzar en circuits oscil·ladors sinusoïdals, pel que s'exposa a continuació.
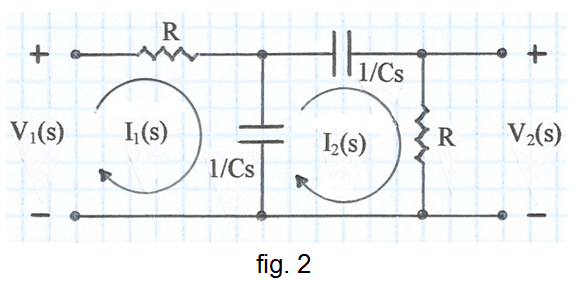
Un cas particular interessant és: Z1 = Z4 = R i Z2 = Z3 = 1 / Cs , que s'indica a la fig. 2.
Substituint valors a (5) i manipulant l'expressió s'arriba a:
Comparant el coeficient de la s del denominador de (6) amb la seva forma estàndard: 3ω0 = 2ξω0 es veu que ξ = 3/2 > 1 llavors, es tracta d'un sistema sobreamortit, i per tant estable, com era d'esperar ja que només consta d'elements passius.
En el domini de la freqüència (s = jω), la (6) és:
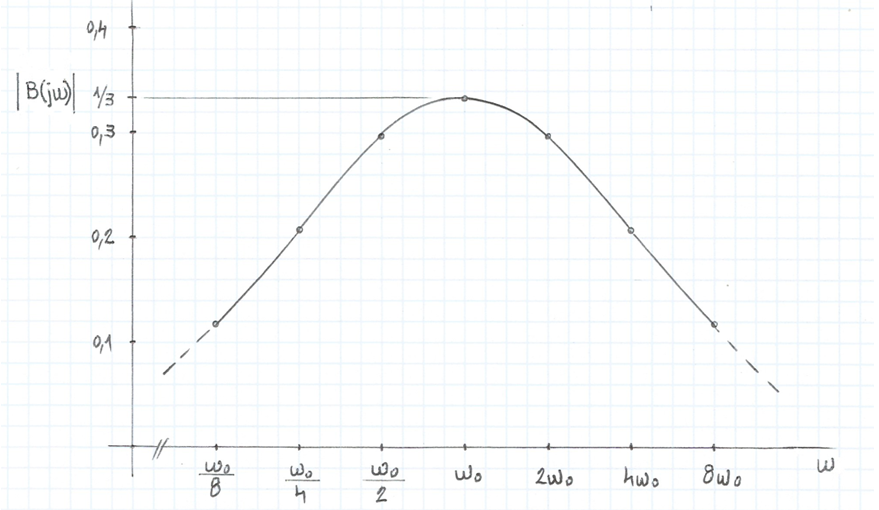
que es representen gràficament a la fig. 3 -comproveu-ho.
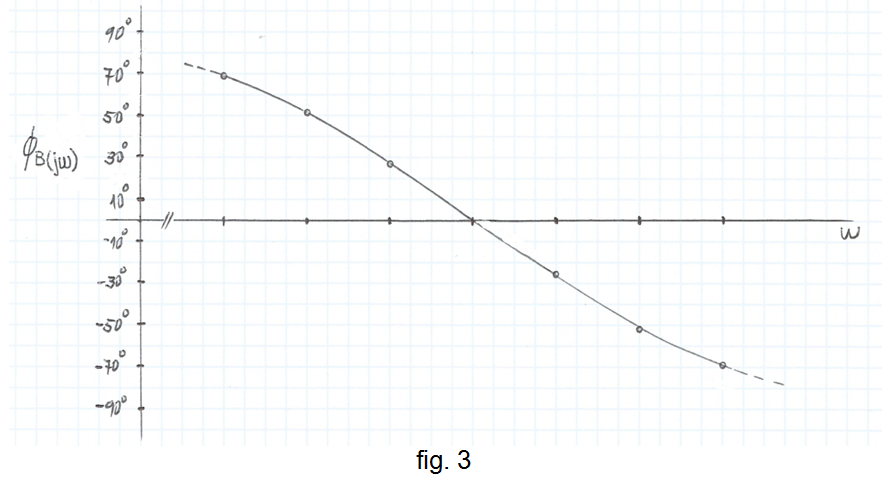
La xarxa és, doncs, un filtre passabanda, centrat a ω0 , on les tensions estan en fase i la sortida val 1/3 de l'entrada. Aquest comportament de la xarxa la fa candidata, com es veurà, a formar part d'un oscil·lador sinusoïdal de freqüència f0 = ω0 / 2π .
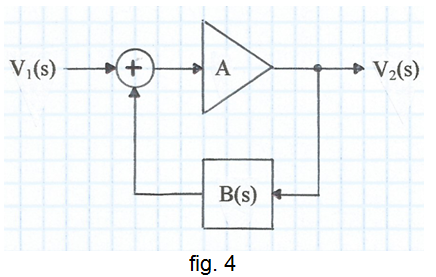
Ara, amb aquesta xarxa fem un sistema realimentat com l'indicat a la fig. 4.
on A és el guany d'un amplificador ideal, és a dir, constant i independent de la freqüència. La funció de transferència d'aquest sistema és:
Substituint (6) a (11) i manipulant l'expressió s'arriba a:
Es poden donar diverses situacions:
• Si el guany A és positiu i inferior a 3 , llavors 0 < ξ = (3-A) / 2 < 3/2 , la resposta serà una sinusoide amortida, superposada a un esglaó d'amplitud A i el sistema serà estable -raoneu-ho.
• Si el guany A és igual a 3 , llavors ξ = 0 , la resposta serà una sinusoide d'amplitud fixa, de freqüència angular ω0 , superposada a un esglaó d'amplitud A i el sistema serà un oscil·lador marginalment estable -raoneu-ho.
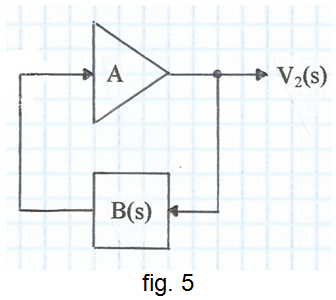
• Si el guany A és superior a 3 però inferior a 5 , llavors -1 < ξ < 0 , la resposta serà una sinusoide l'amplitud de la qual augmentarà amb el temps, superposada a un esglaó d'amplitud A , el sistema serà inestable i es saturarà l'amplificador retallant els pics del senyal generat -raoneu-ho. En aquestes condicions el sistema no necessita senyal d'entrada ja que al connectar la font d'alimentació els transitoris que es generen produeixen l'arrencada de l'oscil·lador -raoneu-ho- i a la fig. 3 es pot suprimir el sumador, tal com s'indica a la fig. 5 .
• Si el guany és superior a 5 , l'amplificador del sistema es satura directament sense oscil·lacions -raoneu-ho.
Així, per obtenir un oscil·lador amb la garantia de que arrenqui, el guany del amplificador haurà de ser una mica més gran que 3 -per exemple un 5% més- el que vol dir acceptar un cert grau de distorsió en el senyal de sortida v2(t) -raoneu-ho.
Expressant la (12) en el domini de la freqüència, tenim:
i a la freqüència ω0 , la (16) serà:
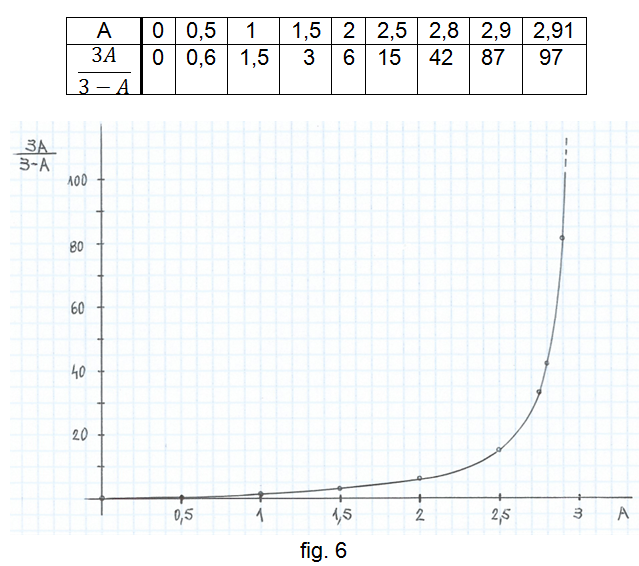
que és el guany del sistema realimentat, a la freqüència ω0 , en funció del guany A de l'amplificador. La següent taula de valors i la seva representació gràfica (fig. 6), ens indiquen que el guany del sistema realimentat augmenta molt de pressa quan el guany A de l'amplificador s'acosta a 3 .
Un altre concepte important a tenir en compte a l'hora de dissenyar un oscil·lador, és l'estabilitat del valor de la freqüència que genera.
A la (11), al producte AB(s) se'n diu guany del sistema en anell obert i hem vist que quan A = 3 passa que AB(jω0) = 3·(1/3) = 1 i el sistema es torna marginalment estable.
En aquestes condicions la fase ØAB(jω) de AB(jω) , que és igual a la fase de B(jω) ja que A és una constant real, hem vist que val zero: ØAB(jωo) = 0 -per a qualsevol xarxa en general, aquesta condició s'amplia dient que val zero o un múltiple de 2π radians -raoneu-ho.
ØAB no depèn només de ω sinó que es pot veure alterada per factors ambientals externs, envelliment de components, etc, que indicarem genèricament com x1, x2, ··· . Així escriurem ØAB(ω, x1, x2, ···). Com que la freqüència ω0 que genera l'oscil·lador ve marcada per la intersecció d'aquesta corba de fase amb l'eix de freqüències, a continuació definirem un factor d'estabilitat del valor ω0 .
Els factors x1, x2, ··· també repercutiran en el guany AB(jω) . Si el guany està prou sobredimensionat, el circuit no deixarà d'oscil·lar enfront d'aquests factors pertorbadors i en tot moment es complirà ØAB = 0 , però apareixerà un desplaçament de la freqüència respecte del valor desitjat. A la fig. 7 s'il·lustren aquestes fluctuacions de la corba de fase que alteren el valor de ω0 .
La (19) ens diu que la variació relativa de freqüència Δω / ω0 que es pugui produir serà tant més petita com més grans siguin la freqüència ω0 i el pendent de la corba de fase en el punt d'intersecció d'aquesta amb l'eix de freqüències. A aquest denominador se n'hi diu factor d'estabilitat SF :
En el cas concret que ens ocupa:
i substituint (28) i (29) a (27), obtenim: SF = -2/3 .
En definitiva; un procediment que se'n deriva d'aquesta anàlisi a l'hora de dissenyar un oscil·lador sinusoïdal, és:
• Utilitzarem un amplificador que a la freqüència desitjada ω0 tingui un guany A que, a efectes pràctics, es pugui considerar un nombre real; ja sigui positiu -amplificador no inversor- o negatiu -amplificador inversor.
• Escollirem una xarxa de realimentació que contingui elements reactius, que a la freqüència desitjada ω0 la tensió de sortida estigui en fase o en oposició amb la tensió d'entrada, és a dir, que el valor de la funció de transferència B(jω) a ω0 sigui un nombre real, ja sigui positiu o negatiu.
• En principi, s'imposa al sistema la condició de marginalment estable, és a dir, que el guany en anell obert a ω0 valgui la unitat: AB(jω0) = 1. Això implica que si B(jω0) > 0, llavors haurà de ser A > 0 i si B(jω0) < 0, llavors haurà de ser A < 0.
• També es veu que el valor mínim del guany haurà de ser: Amín = 1 / B(jω0) , el qual, com hem dit abans, caldrà d'augmentar una mica -per exemple, un 5% més- per assegurar l'arrencada de l'oscil·lador, per la qual cosa s'haurà d'acceptar un cert grau de distorsió del senyal de sortida v2(t) -raoneu-ho.
• Si el valor de SF resulta insuficient per mantenir el grau d'estabilitat desitjat del valor de la freqüència generada, llavors s'ha d'utilitzar una altra xarxa de realimentació que proporcioni un valor absolut de SF més gran.
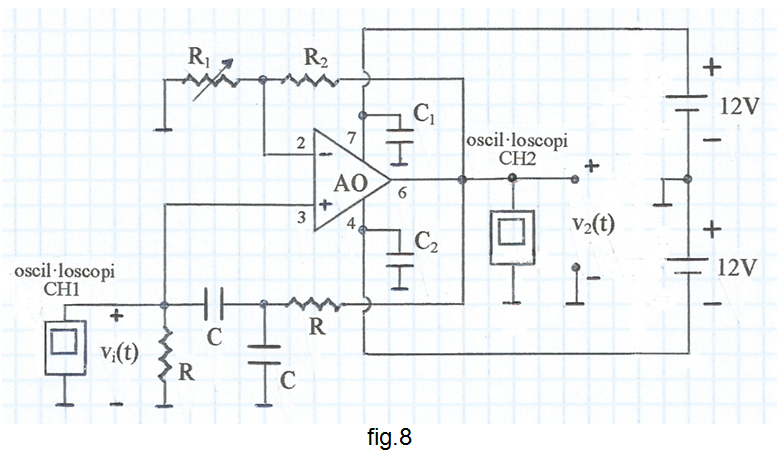
D'acord amb la fig. 5, l'esquemàtic del circuit a assajar s'indica a la fig. 8 .
Totes les resistències són de 0,25W de dissipació. Per obtenir una millor concordança entre les previsions i els resultats obtinguts, la tolerància d'aquestes resistències hauria de ser de l'1% . O també, per a cada resistència, combinar-ne dues del 5% de manera que el valor resultant mesurat s'acosti el més possible al desitjat. Per exemple, dues resistències del 5% de 12kΩ i 68kΩ en paral·lel, donen un valor mesurat molt proper a 10kΩ -comproveu-ho.
De la mateixa manera, quan als condensadors, per a cadascun d'ells se'n poden combinar dos en paral·lel de manera que el valor resultant mesurat s'acosti el més possible al desitjat. Per a minimitzar les pèrdues en els condensadors i els resultats s'acostin el màxim possible a les previsions, cal que, al menys, el dielèctric dels condensadors de major capacitat sigui de plàstic -no ceràmic.
En el muntatge que ha servit per preparar aquesta pràctica, tant per a les resistències com per als condensadors s'han combinat elements en paral·lel.
Relació de components:
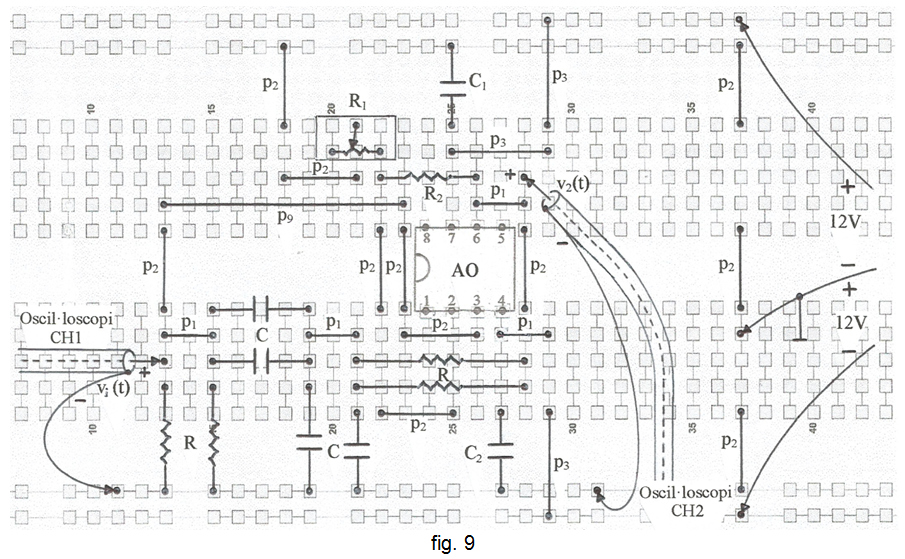
A la fig. 9 s'indica la planificació del muntatge a la protoboard i a la fig. 10 una fotografia.
Procediment:
• Ajusteu R1 al seu màxim valor (100kΩ).
• Aneu disminuint el valor de R1 fins que l'oscil·lador justament arrenqui. Mesureu el valor de la freqüència, que ha ser molt semblant a la prevista.
• Amb el multímetre mesureu el valor real de R2 i el valor real de R1 en aquestes condicions.
• Amb els valors anteriors calculeu el guany de l'amplificador: A = 1 + (R2 / R1) -raoneu-ho-
el qual ha de coincidir sensiblement amb el previst.
• Disminuïu una mica més el valor de R1 per augmentar una mica més el guany, tot observant les tensions v2(t) i vi(t) . Fixeu el grau de distorsió per a v2(t) de manera que, engegant i parant l'oscil·lador, l'arrencada quedi assegurada.
• Observeu l'efecte de filtre passabanda de la xarxa de realimentació a la vista de les formes d'ona de les tensions v2(t) i vi(t).