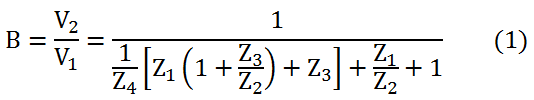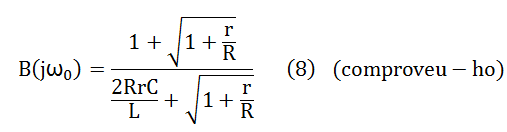Aquest tipus d'oscil·lador s'utilitza freqüentment per a altes freqüències (HF) i els elements actius acostumen a ser transistors, ja siguin bipolars (BJT) o d'efecte de camp (FET). Això no obstant, i a la fi de poder comparar el seu funcionament amb els oscil·ladors sinusoïdals anteriors, en aquesta pràctica s'emprarà un amplificador operacional (AO) que es farà treballar a freqüències molt més baixes.
La topologia de la xarxa de realimentació d'aquests tipus d'oscil·ladors és la mateixa que l'emprada a l'anterior pràctica Oscil·ladors sinusoïdals (1). L'expressió general de la funció de transferència d'aquesta xarxa es recorda a continuació:
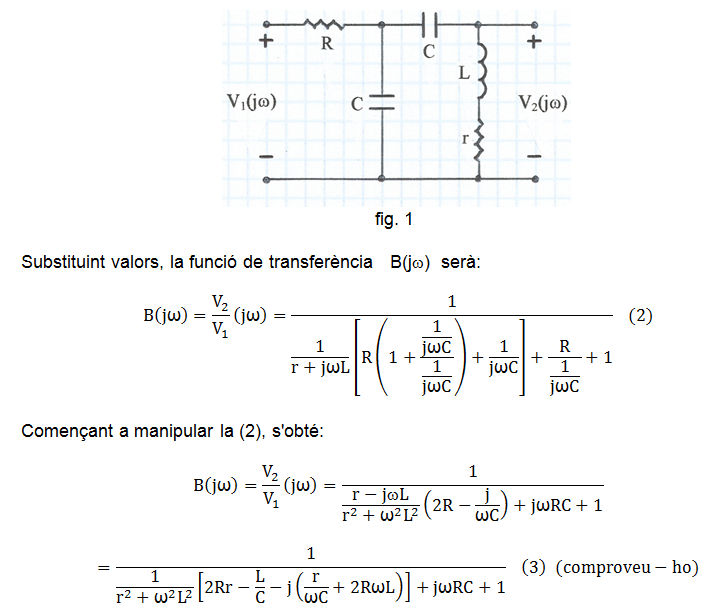
En aquesta pràctica, Z1 = R , Z2 = Z3 = 1 / jωC i Z4 = r + jωL on r representa la resistència equivalent en sèrie de les pèrdues de la bobina. A la fig. 1 s'indica l'esquemàtic d'aquesta nova xarxa.
Normalment les inductàncies es fan treballar a freqüències a les quals es compleix r << ωL amb la qual cosa, i amb més raó, es complirà que r2 << ω2L2 i això permet menystenir r2 en front de ω2L2 i simplificar la (3). Fent aquesta simplificació i separant les parts real i imaginària del denominador, finalment s'obté:
Observació: si haguéssim considerat la bobina com un element ideal (r = 0) la (5) seria:
i la (7) ens diu que: 1) a la freqüència ω0 la tensió de sortida de la xarxa de realimentació és del mateix signe que la tensió d'entrada i 2) de valor doble que aquesta, la qual cosa es deu a la ressonància. Com a conseqüència de tot això, l'amplificador a emprar haurà de tenir un guany de tensió inferior a la unitat; de només 1/2 -raoneu-ho-, és a dir, podria ser un AO configurat com seguidor o un BJT com seguidor d'emissor o un FET com seguidor de font, seguits algun tipus d'atenuador de sortida.
Tornant al cas real de la bobina amb pèrdues, substituint (5) a la part real del denominador de (4), obtenim:
Observació: tornant momentàniament al cas ideal de la bobina sense pèrdues, si substituïm r = 0 a la (8) obtenim la (7), com era d'esperar.
Tornant al cas real de la bobina amb pèrdues, per a que B(jω0) sigui superior a 1 , la (8) ens diu que s'hauria de complir 2RrC/L < 1 (9) -raoneu-ho-, llavors, per a uns valors donats de C , r i L , si fem R variable podrem actuar sobre l'atenuació del sistema per fixar el grau de distorsió del senyal de sortida generat per l'oscil·lador. Observeu que com més petit sigui el valor de R més gran serà B(jω0) .
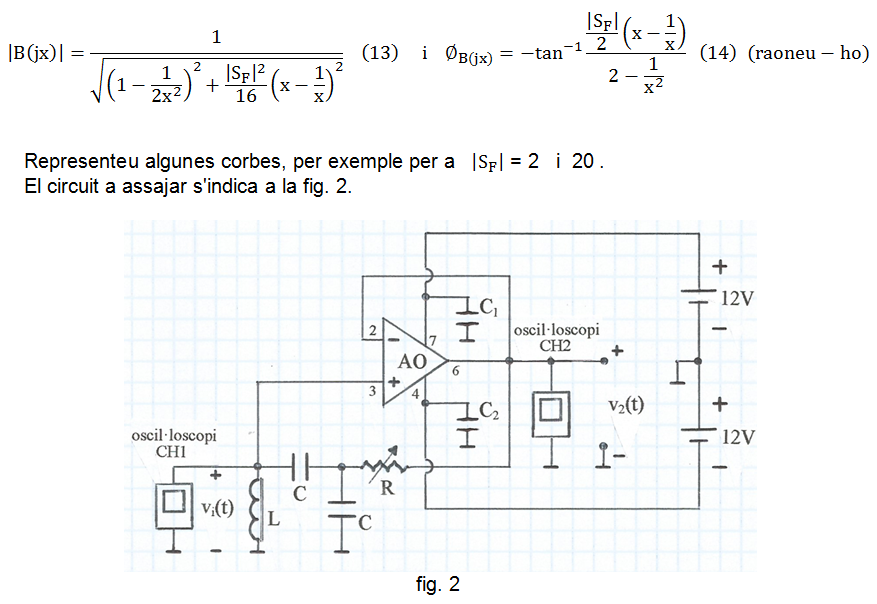
Per calcular el factor d'estabilitat i representar les corbes de guany i fase ho farem per al cas ideal sense pèrdues (r = 0) ; així, la (4) seria:
El guany i la fase de B(jx) seran:
Procediment:
• Escolliu els dos condensadors C de manera que els seus valors reals siguin el més semblants possible. Feu la mitjana d'aquests dos valors, que prendrem com el valor real de C .
• Mesureu el valor real de L i el valor de la resistència òhmica del conductor amb el qual està construïda, que serà una aproximació per defecte del valor de r ja que en aquesta mesura no estan incloses les pèrdues en el nucli -raoneu-ho.
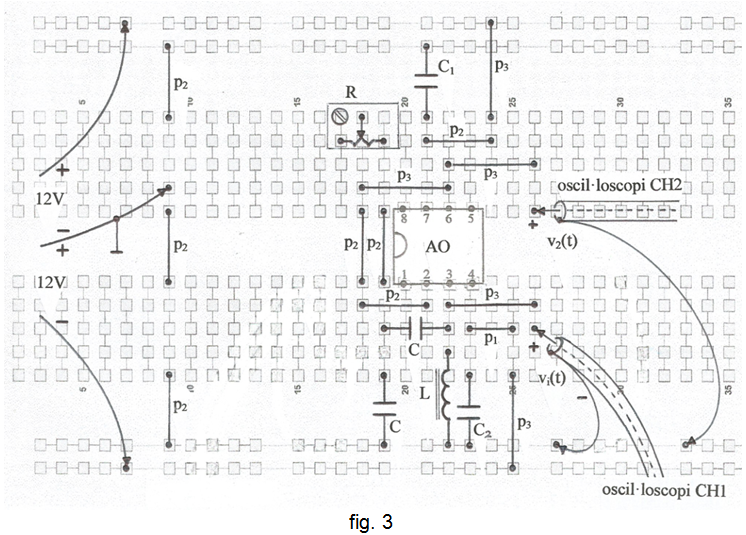
A la fig. 3 s'indica una planificació del muntatge a la protoboard i a la fig. 4, la fotografia.