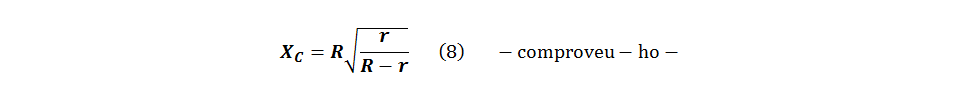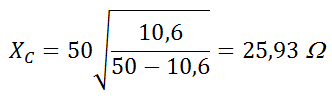Abans de fer aquesta pràctica cal haver fet, o al menys llegit, l'anterior pràctica: Analitzador de xarxes. Comportament de resistències, capacitats i inductàncies amb la freqüència.
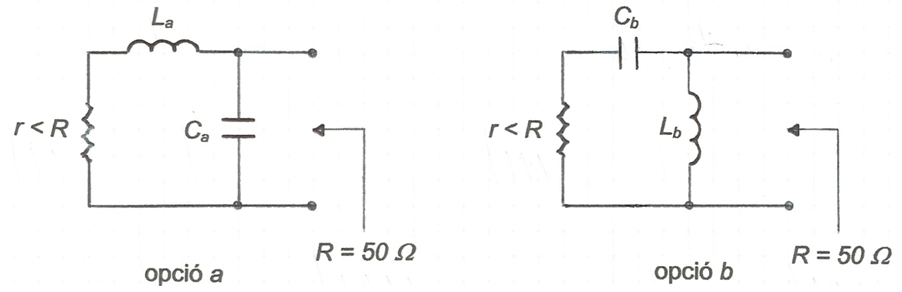
Per a una freqüència determinada, es tracta d'adaptar una càrrega resistiva r < 50 Ω a un dispositiu la impedància interna del qual és R = 50 Ω resistius. Una possibilitat -la més simple- és emprar una xarxa en "L" com la indicada a la fig. 1 on es poden veure dues opcions.
fig. 1
Els subíndexs a i b indiquen que els valors d'inductància i capacitat depenen de l'opció escollida. Farem la pràctica emprant l'opció a tal com s'indica a la fig. 2 on, per simplificar la notació, prescindirem dels subíndexs.
fig. 2
que són les mateixes fórmules obtingudes a la pràctica: Xarxa adaptadora d'impedàncies en "L" , com era d'esperar -raoneu-ho.
El plantejament directe del problema és: donats els valors de R , r i f s'han de determinar els valors de L i C per aconseguir l'adaptació. Per exemple, si R = 50 Ω i r = 10 Ω , substituint aquests valors a (7) i (8) s'obté: XL = 20 Ω i XC = 25 Ω . Si la freqüència a la qual volem aconseguir l'adaptació és, per exemple f = 1 MHz , la inductància i la capacitat necessàries valen:
Davant de la dificultat d'obtenir aquests valors per poder fer la pràctica i comprovar que les previsions es compleixen, s'opta per seguir un altre camí més fàcil que igualment ens permetrà comprovar el funcionament que s'espera de la xarxa d'adaptació. Els valors nominals estandarditzats més propers als desitjats són 3,3 μH i 6,8 nF . Emprant, doncs, aquests components mesurem els seus valors reals a la freqüència d'1 MHz i resulten, per exemple 3,5 μH i 6,5 nF . A més, la resistència sèrie equivalent de pèrdues de la bobina -resistència òhmica i pèrdues en el nucli- a aquesta freqüència resulta d'uns 0,4 Ω . Quan al condensador, se'l pot considerar un element ideal, és a dir, sense pèrdues, en front de les pèrdues de la bobina.
El component més fàcil d'ajustar és la resistència r ja que podem emprar una resistència variable o bé tantejar combinant resistències en sèrie o en paral·lel per aconseguir el valor necessari. En aquesta pràctica seguirem el mètode de combinar resistències en paral·lel.
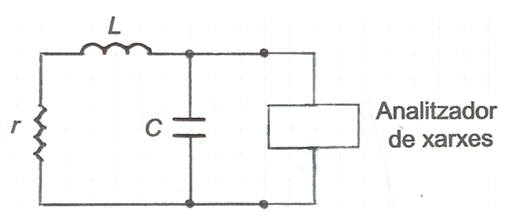
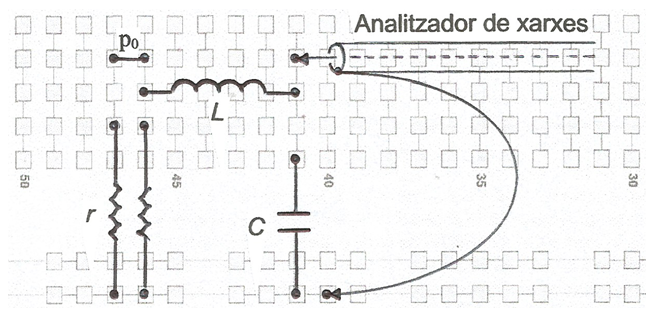
A la fig. 3 s'indica la planificació del muntatge i a la fig. 4, una fotografia.
fig. 3
fig. 4
Relació de components:
Les resistències són de 0,25 W de dissipació i del 5 % de tolerància.
Procediment:
• Disposeu l'analitzador de xarxes en format carta de Smith i fixeu un marge de freqüències adequat, per exemple des de la freqüència mínima que permet l'analitzador fins al voltant del doble de la freqüència d'adaptació.
• Abans de muntar el circuit s'ha de procedir a la calibració del conjunt format per l'analitzador, el cable coaxial que el connecta a la protoboard i la protoboard, a fi d'obviar les capacitats i inductàncies paràsites que el cable i la protoboard introdueixen. Aquesta calibració s'explica a l'anterior pràctica: Analitzador de xarxes. Comportament de resistències, capacitats i inductàncies amb la freqüència
Un cop feta la calibració munteu el circuit a assajar i prosseguiu.
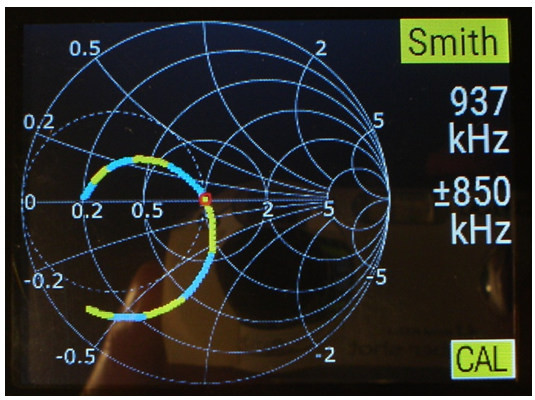
• Ajusteu el valor de r fins aconseguir que la gràfica passi pel centre de la carta de Smith (fig. 5). A la fig. 4 es veu que això s'ha aconseguit amb dues resistències en paral·lel de valors nominals 12 Ω i 68 Ω . El valor real mesurat ha coincidit sensiblement amb el nominal: r = 12 // 68 = 10,2 Ω .
fig. 5
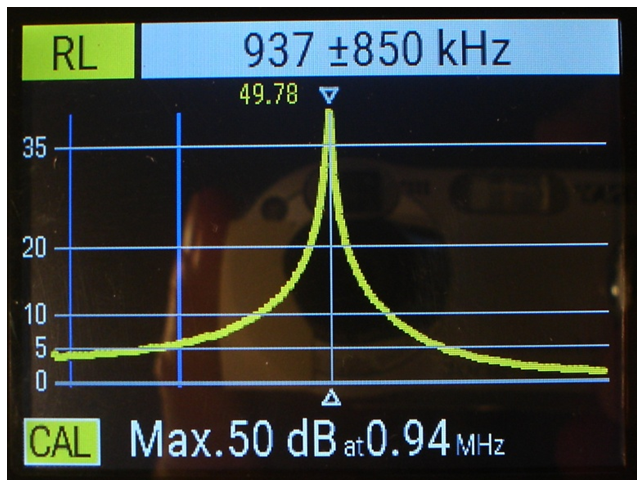
• El cursor de la carta de Smith -petit quadrat vermell- ens indica que la freqüència d'adaptació és d'uns 937 kHz .
• Anem a comprovar que aquesta freqüència està d'acord amb les previsions teòriques. A partir de (7) i (8) podem trobar la freqüència -que serà de ressonància- per a uns determinats valors de R, r, L i C . Com que:
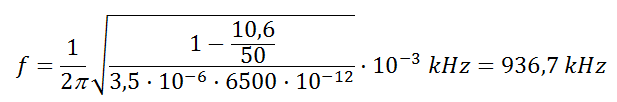
resultat gaire bé idèntic al trobat.
Observacions:
• Recordeu que la gràfica de la carta de Smith evoluciona amb la freqüència en el sentit de les busques del rellotge.
• Amb la normalització a 50 Ω , a les freqüències més baixes la gràfica arrenca aproximadament a 10,6 / 50 = 0,212 Ω normalitzats resistius, com es veu a la carta.
• El centre de la carta correspon a la resistència normalitzada d'1 Ω , és a dir, 1·50 = 50 Ω .
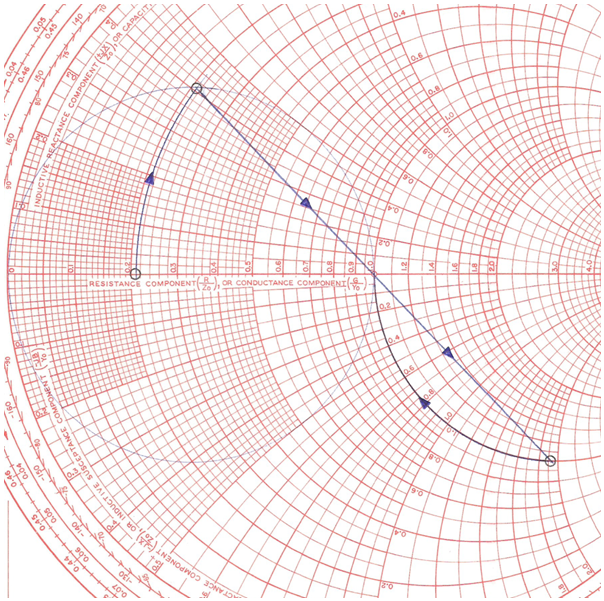
Com exercici, podem emprar una carta de Smith per justificar de manera gràfica els valors dels components emprats (fig. 6).
fig. 6
• Aquest procediment gràfic arrenca amb la r normalitzada de 0,212 Ω , a la qual se li afegeix una reactància inductiva fins que talli a una circumferència de radi la unitat i que ha de correspondre a un valor normalitzat de:
com, efectivament, es pot llegir a la carta.
• A continuació es troba l'admitància normalitzada corresponent a la impedància normalitzada 0,212 + j 0,409 Ω :
com, efectivament, es pot llegir a la carta.
• Finalment, a l'admitància anterior se li ha d'afegir una susceptància capacitiva de 1,927 S per a que el resultat final sigui una admitància real d'1 S , és a dir, una resistència normalitzada d'1 Ω a la que correspon un valor de resistència de 50 Ω , que és el resultat desitjat.
• La reactància normalitzada corresponent a la susceptància capacitiva anterior val : 1/1,927 = 0,519 Ω , és a dir, una reactància de 50·0,519 = 25,95 Ω , la qual cosa ha d'estar d'acord amb (8) :
com era d'esperar.
Si es va en compte amb la utilització de la carta de Smith es poden obtenir valors de components prou acurats.
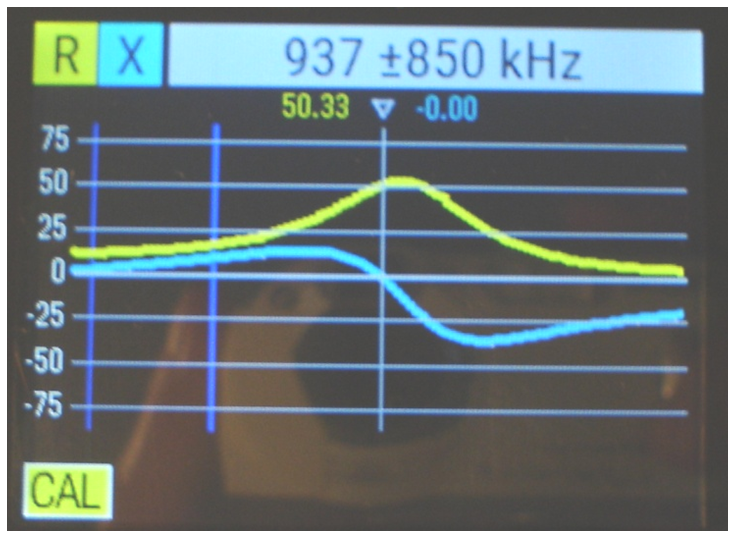
Altres formats de presentació de resultats de l'analitzador de xarxes poden ser, per exemple, la variació de les parts real i imaginària amb la freqüència (fig. 7).
fig. 7
O les pèrdues de retorn (fig. 8)
fig. 8
O la relació d'ona estacionària (fig. 9), que l'analitzador emprat permet dues presentacions.
fig. 9
i encara altres presentacions.
Suggeriments:
• Assageu l'adaptació per a altres valors de r , per exemple al voltant de 15 Ω , 18 Ω , 22 Ω , etc.