Es tracta de comprovar com varia el valor d'una resistència amb la temperatura. L'increment de la seva temperatura, a conseqüència del corrent per ella, és proporcional a la potència que la resistència dissipa -raoneu-ho.
A la fig. 1 s'indiquen dues resistències de 100 Ω que s'utilitzaran per fer els assajos . La resistència de l'esquerra és de pel·lícula de grafit, d'1 W de dissipació, i la de la dreta és bobinada, de 4 W de dissipació. La capacitat de dissipació del calor generat en una resistència, és proporcional a la seva superfície -raoneu-ho. A la figura s'indica també com s'han doblegat els terminals de les resistències per inserir-les a la protoboard de forma correcta.
Recordatori:
Si una resistència té un valor R1 a una temperatura t1 , el seu valor R2 a una temperatura t2 es pot aproximar per la fórmula:
on α és el coeficient de temperatura el qual depèn del material amb què està construïda. Per a les resistències de pel·lícula de grafit α < 0 , per la qual cosa el seu valor disminueix amb la temperatura. Per a les resistències bobinades, l'aliatge del fil amb què estan construïdes té un α > 0 , per la qual cosa el seu valor augmenta amb la temperatura.
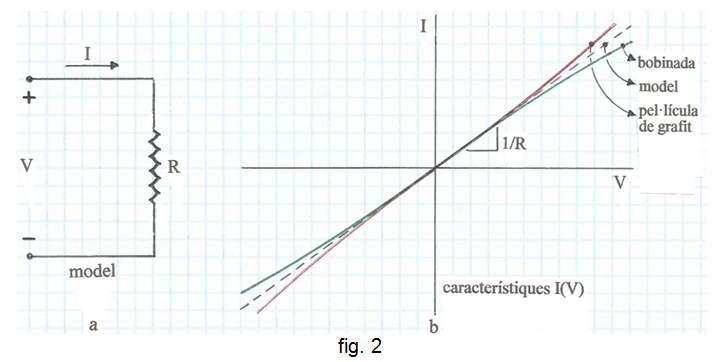
A la fig. 2a es representa el model de resistència lineal, que no depèn de la temperatura, i a la fig. 2b es comparen els comportaments reals de les resistències amb la temperatura, amb el del model.
Els sentits de referència associats, per a la tensió i el corrent de la fig. 2a, serveixen per convenir que quan els sentits de la tensió aplicada i del corrent elèctric per la resistència coincideixen amb les referències, la característica I(V) es representa en el 1r quadrant. Si s'inverteix la tensió aplicada, el sentit del corrent també s'invertirà, llavors ambdós seran oposats a les referències i I(V) es representa en el 3r quadrant.
La fig. 2b ens mostra, doncs, funcions senars, és a dir, funcions que compleixen: I(-V) = -I(V) (raoneu-ho).
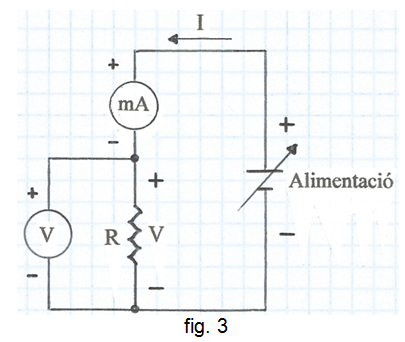
Per comprovar tot això s'emprarà el circuit de la fig. 3. S'observa que el voltímetre està en paral·lel amb la resistència R . Si la resistència interna RV del voltímetre és molt més gran que R , per exemple RV = 10 MΩ i R = 1 kΩ , llavors el corrent indicat per l'amperímetre és pràcticament el que passa per R , en conseqüència la presència del voltímetre no introduirà errors apreciables en la determinació del seu valor -raoneu-ho.
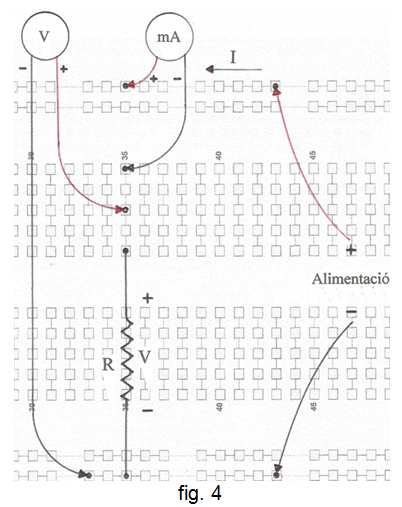
A la fig. 4 s'indica la planificació del muntatge a la protoboard i a la fig. 5, una fotografia.
Relació de components:
Procediment:
• Comenceu per la resistència de 100 Ω/1 W de pel·lícula de grafit, mesurant el seu valor real amb un multímetre.
• Munteu el circuit i seleccioneu les escales de 20 V per al voltímetre i 200 mA per a l'amperímetre. Aquestes escales es mantindran durant tot l'assaig a la fi d'evitar els errors inherents als instruments que es produeixen quan es fan canvis d'escales.
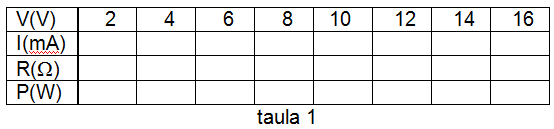
• Confegiu una taula de valors com s'indica a la taula 1 ajustant els valors de les tensions al voltant dels indicats -no cal capficar-se en ajustar els valors exactament als indicats. Es van prenent els valors del corrent per a cadascuna de les tensions ajustades i es van calculant els valors de resistència R = V / I i de la potència absorbida i dissipada per aquesta P = V·I
El valor de R calculat amb la tensió més baixa ha de coincidir sensiblement amb el mesurat amb el multímetre.
COMPTE!: la temperatura de la resistència va augmentant amb la potència, llavors s'ha d'anar en compte de no cremar-se si accidentalment la resistència té contacte amb la pell. S'observarà que quan la resistència s'escalfa considerablement, aquesta desprèn una olor característica, la qual cosa serveix d'alerta.
Es veurà que a partir d'uns 10 V la potència supera la màxima capacitat de dissipació de la resistència (1 W), això no obstant, l'assaig es pot continuar fins l'última tensió tabulada, emprant el mínim temps possible. Finalment pareu la font d'alimentació per a que la resistència es refredi.
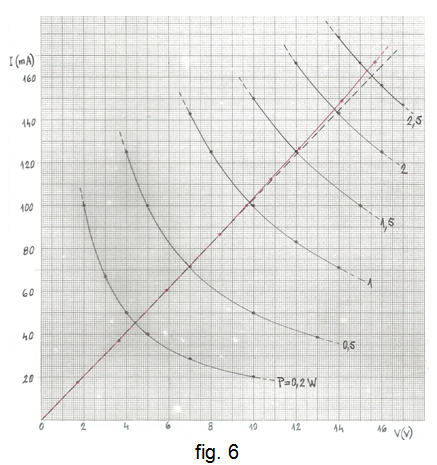
• Sobre paper mil·limetrat o quadriculat representarem la gràfica I(V). Amb l'origen i els dos primers punts representats -quan la resistència pràcticament no s'escalfat encara- traceu la recta amb traç discontinu, que correspondrà al model de resistència que no varia amb la temperatura.
• Representeu la resta de punts obtinguts i dibuixeu la gràfica resultant per comprovar que aquesta queda per sobre de la línia discontínua degut a la disminució de la resistència amb la temperatura.
• Dibuixeu també les gràfiques (hipèrboles) de potència constant P = V·I = Cnt per als valors de P : 0,2 W - 0,5 W - 1 W - 1,5 W - 2 W i 2,5 W . A la fig. 6 es mostra una possible representació de les gràfiques.
• Invertiu la polaritat de la tensió aplicada a la resistència per comprovar que les lectures dels multímetres apareixen precedides pel signe menys, situació que correspon al 3r quadrant, encara que en valor absolut són coincidents amb les anteriors.
• Amb la resistència ja freda -a la temperatura ambient- mesureu de nou el seu valor amb el multímetre, el qual ha de coincidir sensiblement amb el mesurat al principi. Això serveix per comprovar que, tot i el sobreescalfament a que ha estat sotmesa, la resistència està en bon estat.
· Continueu amb la resistència bobinada de 100 Ω/4 W mesurant el seu valor real amb un multímetre.
• Seleccioneu les escales de 200 V per al voltímetre i de 20 A per a l'amperímetre. Igual que abans, aquestes escales es mantindran durant tot l'assaig a fi d'evitar els errors inherents als instruments, que es produeixen quan hi ha canvis d'escales. Amb aquestes escales no s'obtindrà tan bona resolució com amb l'assaig anterior, però serà suficient per constatar l'augment de la resistència amb la temperatura.
• Confegiu una taula de valors com s'indica a la taula 2 ajustant els valors de les tensions al voltant dels indicats -igual que abans, no cal capficar-se en ajustar aquests valors exactament als indicats. Es van prenent els valors del corrent per a cadascuna de les tensions ajustades i es van calculant els valors de resistència R = V/I i de la potència absorbida i dissipada per aquesta P = V·I .
El valor de R calculat amb la tensió més baixa ha de coincidir sensiblement amb el mesurat amb el multímetre.
COMPTE!: igual que abans, la temperatura de la resistència va augmentant amb la potència, llavors s'ha d'anar en compte de no cremar-se si accidentalment la resistència té contacte amb la pell. S'observarà que quan la resistència s'escalfa considerablement, aquesta desprèn una olor característica, la qual cosa serveix d'alerta.
Es veurà que a partir d'uns 20 V la potència supera la màxima capacitat de dissipació de la resistència (4 W), això no obstant, l'assaig es pot continuar fins l'última tensió tabulada, emprant el mínim temps possible. Finalment pareu la font d'alimentació per a que es refredi la resistència.
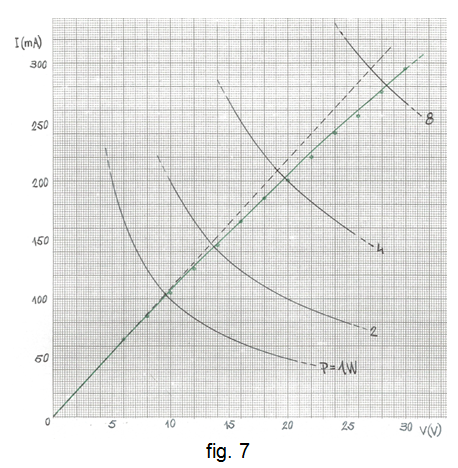
• Sobre paper mil·limetrat o quadriculat representarem la gràfica I(V). Amb l'origen i els dos primers punts representats -quan la resistència pràcticament no s'escalfat encara- traceu la recta amb traç discontinu que correspondrà al model de resistència que no varia amb la temperatura.
• Representeu la resta de punts obtinguts i dibuixeu la gràfica resultant per comprovar que aquesta queda per sota de la línia discontínua a conseqüència de l'augment de la resistència amb la temperatura.
• Dibuixeu també unes quantes gràfiques -hipèrboles- de potència constant P = V·I = Cnt fins P = 8 W. A la fig. 7 es mostra una possible representació d'aquestes gràfiques.
• Igual que abans, invertiu la polaritat de la tensió aplicada a la resistència per comprovar que les lectures dels instruments canvien de signe, encara que en valor absolut són iguals que les anteriors.
• Igual que abans, amb la resistència ja freda -a la temperatura ambient- mesureu de nou el seu valor amb el multímetre, el qual ha de coincidir sensiblement amb el mesurat al principi. Això serveix per comprovar que, tot i el sobreescalfament a que ha estat sotmesa, la resistència està en bon estat.
Observacions:
• Combinant adequadament resistències amb coeficients de temperatura de signe oposat, es poden aconseguir resistències que siguin pràcticament independents de la temperatura, la qual cosa té aplicacions en circuits d'instrumentació i d'altres.
• En la majoria de circuits electrònics interessa que els valors de les resistències no es vegin afectats per la temperatura, llavors les resistències es fan treballar bastant per sota de la seva capacitat de dissipació màxima.
• La fórmula anterior (1) és aproximada; en rigor el valor de la resistència Rt d'un conductor a la temperatura t ve donada per un desenvolupament en sèrie:
on R0 és la resistència a zero graus centígrads i α, β, γ, ··· són coeficients de temperatura. Si una resistència es fa treballar bastant per sota de la seva capacitat de dissipació màxima, el seu comportament s'aproxima molt al d'una resistència lineal, és a dir, la seva característica I(V) és aproximadament un tram rectilini que passa per l'origen, com la del model de resistència lineal de la fig. 2a .
Articles/enllaç d'interès: codi colors interactiu (cal fer servir plugin adobe flash)