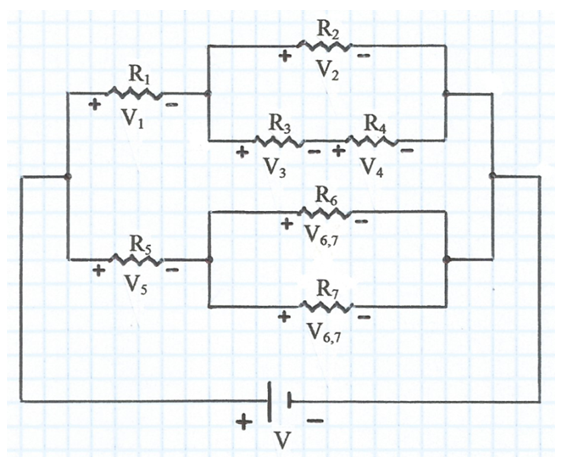
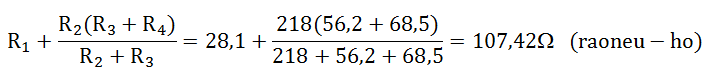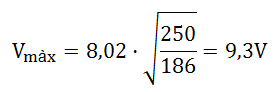A la fig. 1 s'indica una xarxa de resistències connectada a una font d'alimentació de tensió contínua de valor   V    i les caigudes de tensió en borns de cada resistència.

fig. 1

            Es tracta de:

          1. Calculeu i comproveu amb un multímetre la resistència equivalent de la xarxa, és a dir, la resistència que "veu" la font, i la potència que aquesta proporciona.

            2. Amb el multímetre, comproveu la llei de Kirchhoff de les tensions en tots els llocs de la xarxa on es pugui comprovar.

            3. Calculeu la potència que dissipa cada resistència i comproveu que la suma de les potències dissipades per les resistències és igual a la potència entregada per la font.

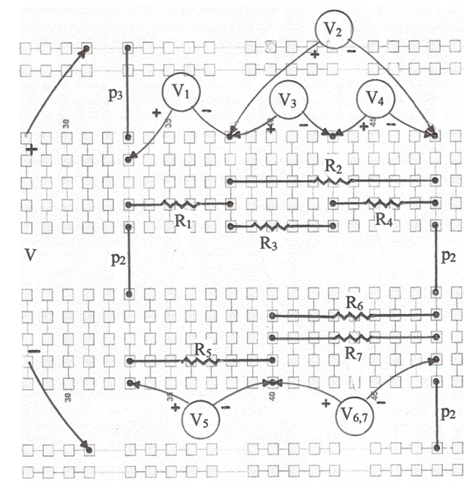
            A la fig. 2 s'indica la planificació del muntatge a la  protoboard  i com fer les mesures de les tensions amb un multímetre, anant-lo connectant en els llocs que s'indiquen. La fig. 3 és una fotografia del muntatge.

fig. 2

fig. 3

            Totes  les  resistències  poden  ser  del  tipus  de  pel·lícula  de  grafit,  del   5 %   de  tolerància i de  0,25 W  de capacitat de dissipació tèrmica, tal com s'indica a la fotografia. 

            Relació de components i aparells:

            Procediment:

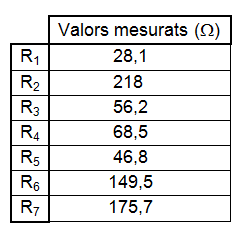
            • Mesureu el valor real de cadascuna les resistències amb el multímetre, i surt, per exemple:

           • Amb els valors mesurats, calculeu la resistència equivalent    Req   de la xarxa de resistències:

            La resistència equivalent de les resistències  R1 ,  R2 ,   R3  i  R4 , val:

            La resistència equivalent de les resistències  R5 ,  R6  i  R7 , val:

           La resistència equivalent   Req  de tota la xarxa de resistències, val:

            • Mesurant amb el multímetre  R_eq  surt, per exemple,  R_eq = 58,4 Ω ,  valor pràcticament igual al calculat anteriorment, com era d'esperar.

            • Alimenteu la xarxa de resistències amb una tensió d'uns  8 V .  Amb el multímetre, emprant l'escala de  20 V  i sense canviar d'escala, mesureu la tensió d'alimentació i les caigudes de tensió en cadascuna de les resistències, i surt, per exemple:

            • Comproveu la llei de Kirchhoff de tensions allà on es pugui comprovar:

                               V₃ + V₄ = 2,64 + 3,23 = 5,87V ≅ V₂ = 5,9 V ,   com era d'esperar.

                               V₁ + V₂ = 2,11 + 5,9 = 8,01V ≅ V = 8,02 V ,   com era d'esperar.

                               V₅ + V_6,7 = 2,95 + 5,08 = 8,03V ≅ V = 8,02 V ,    com era d'esperar.

            • La potència entregada per la font val:   P = V²/R_eq = 8,02²/58,4 = 1.101,4 mW .

            • Les potències dissipades per cadascuna de les resistències, valen:

            P₁ = 2,11² / 28,1 = 158,4 mW;       P₂ = 5,9² / 218 = 159,7 mW;        P₃ = 2,64² / 56,2 = 124 mW

            P₄ = 3,23³ / 68,5 = 152,3 mW;       P₅ = 2,95² / 46,8 = 186 mW;        P₆ = 5,08² / 149,5 = 172,6 mW

            P₇ = 5,08² / 175,7 = 146,9 mW .

            La suma de potències dissipades, val:

            158,4 + 159,7 + 124 + 152,3 + 186 + 172,6 + 146,9 = 1.100 mW ,  valor pràcticament igual a la potència  P  entregada per la font, com era d'esperar.

            • Suposant que les resistències es comporten com elements ideals -lineals-, és a dir, que els seus valors no varien amb la temperatura, ¿quin és el valor màxim  V_màx  de la tensió d'alimentació que és pot aplicar, sense superar la capacitat de dissipació tèrmica de cap de les resistències?

            Resposta:

            La resistència  R₅  és la que dissipa més potència, llavors, aquesta resistència serà la que marcarà el límit de la màxima tensió a aplicar:

            Efectivament; a l'augmentar la tensió d'alimentació  V  de  8,02 V  a  9,3 V , la tensió  V₅  en borns de  R₅  augmentarà fins:

i la potència que dissiparà  R₅  serà:  3,42² / 46,8 = 0,25 W , com era d'esperar -raoneu tot això.

            Suggeriment: assageu amb altres valors de resistències i altres valors de la tensió d'alimentació.

Escriure un comentari