L'analitzador de xarxes que s'utilitzarà en les pràctiques on aparegui aquest instrument serà el model AA-55 ZOOM del fabricant RigExpert. El seu marge de freqüències va de 60 kHz a 55 MHz i es un instrument pensat per a radioafeccionats, per ajustar antenes, fer mesures en línies de transmissió, etc.
Òbviament, també resulta útil per fer mesures en circuits amb constants concentrades -resistències, capacitats, inductàncies, etc.- i tot el què es digui aquí es podrà fer amb qualsevol altre analitzador de xarxes.
Abans de començar a fer mesures s'ha de fixar el marge de freqüències que ens interessa, i després cal fer una calibració amb el conjunt format per l'analitzador, el cable coaxial que el connecta a la protoboard i la protoboard. Tot això a fi d'obviar les capacitats i inductàncies paràsites que el cable i la protoboard introdueixen i que podrien falsejar les mesures que es facin.
Suposant que ens interessi tota la gamma de freqüències que permet aquest analitzador, fixarem la freqüència central:
Un cop connectat l'analitzador al cable i aquest a la protoboard, seguiu les instruccions del manual de l'analitzador per fer la calibració prèvia, que vindrà a dir:
1) Inseriu un circuit obert, és a dir, cap component, i introduïu la dada a l'aparell.
2) Inseriu un curtcircuit, és a dir, un pont entre els terminals del cable coaxial, que haurà de ser el més curt possible, i introduïu la dada a l'aparell.
3) Inseriu una resistència de 50 Ω , amb terminals el més curts possible, i introduïu la dada a l'aparell (50 Ω és el valor que normalment es fa servir per normalitzar la carta de Smith, encara que també es fan servir altres valors, com 25 Ω , 75 Ω o 100 Ω ).
La relació de components emprats per fer aquesta pràctica és:
Les resistències poden ser de 0,25 o 0,5 W de dissipació.
A la fig. 1 s'indica la situació de circuit obert. A la fig.2 la d'un curtcircuit, el qual es fa amb el pont p3. A la fig.3 la de la càrrega de 50 Ω , la qual es fa amb les dues resistències de 100 Ω connectades en paral·lel mitjançant el pont p0. Prèviament s'hauran escollit les resistències de manera que el seu valor real s'acosti el màxim possible als 50 Ω .
fig. 1
fig. 2
fig. 3
A continuació assajarem la resta de resistències, els condensadors i les bobines.
A la fig. 4 s'indiquen dues resistències idèntiques de 27 Ω ; una amb els terminals escurçats i l'altra amb la seva longitud original, molt més llargs.
fig. 4
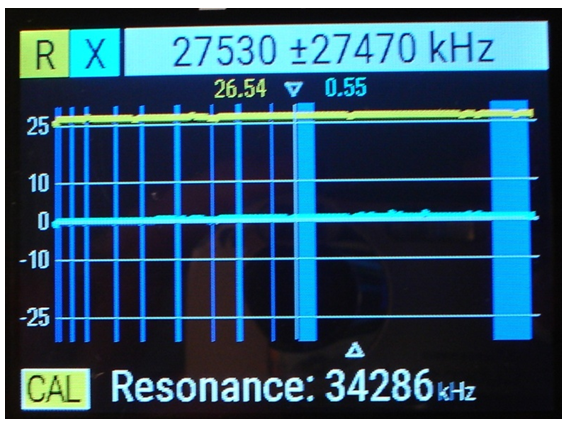
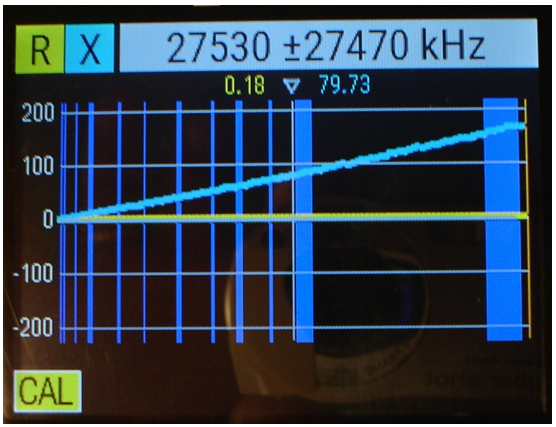
La fig. 5 correspon a la resposta en freqüència, en format RX, de la resistència de terminals escurçats, i observeu:
fig. 5
• El valor de la resistència es manté gaire bé constant amb la freqüència.
• S'aprecia una lleugera reactància inductiva paràsita en sèrie, la qual es manté inferior a 1 Ω .
• Un cursor indica els valors de resistència i reactància a la freqüència central de 27.530 kHz : R = 26,54 Ω i XL = 0,55 Ω .
• Un altre cursor indica que a 34.286 kHz l'analitzador detecta una anul·lació de XL , la qual cosa la interpreta com una ressonància sèrie.
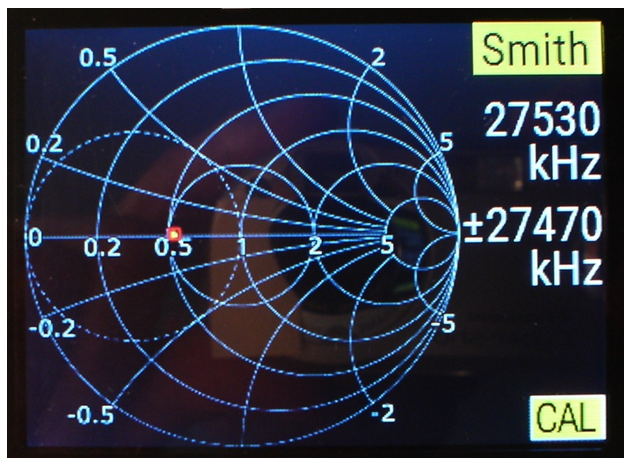
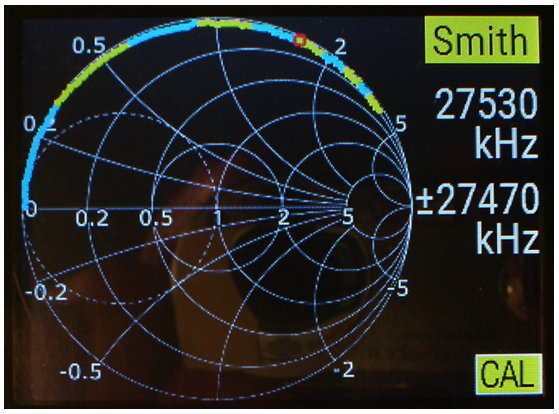
La fig. 6 correspon a la resposta en freqüència de la resistència en format carta de Smith, i observeu:
fig. 6
• El cursor -petit quadrat vermell- ens indica una part resistiva de valor lleugerament superior a 0,5·50 = 25 Ω , i una part reactiva gaire bé nul·la en tota la gamma de freqüències.
A continuació s'assaja el comportament amb la freqüència de la resistència de terminals llargs, i observeu:
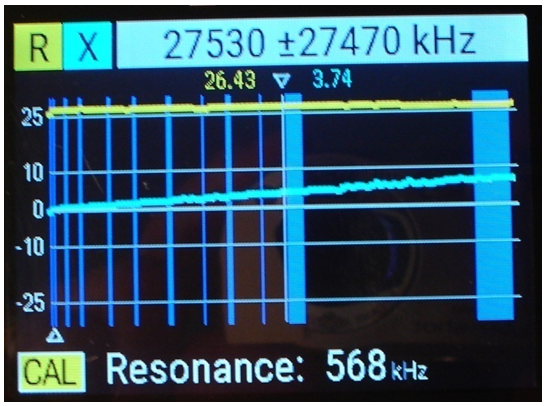
fig. 7
• En format RX (fig. 7) la part resistiva es manté, igual que abans, sensiblement constant amb la freqüència.
• Quan a la part reactiva, la inductància paràsita afegida per la major longitud dels terminals fa que la component de reactància inductiva augmenti. Movent el cursor per prendre lectures a diverses freqüències, es constata que la reactància augmenta gaire bé linealment amb la freqüència, fins a un valor d'uns 7 o 8 Ω a la màxima freqüència de mesura.
• Igual que abans, l'analitzador detecta una anul·lació de la reactància a 568 kHZ , la qual cosa la interpreta com una ressonància sèrie.
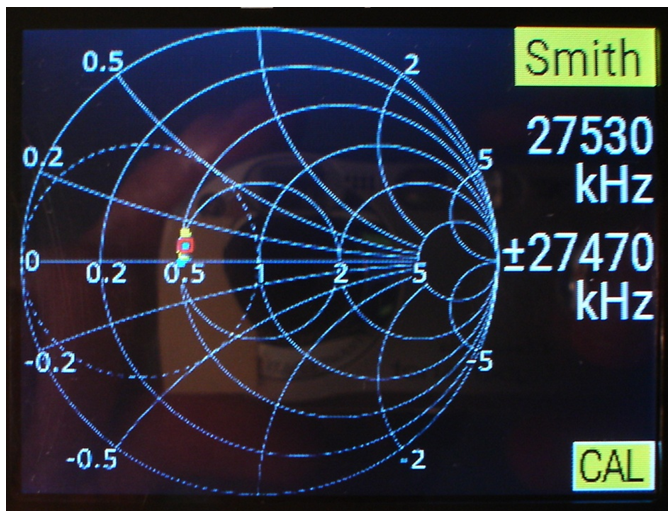
La fig. 8 correspon a aquesta segona resistència en format carta de Smith, i observeu:
fig. 8
• Es veu que la seva part resistiva evoluciona amb la freqüència gaire bé damunt d'una circumferència de valor lleugerament superior als 0,25·50 = 25 Ω .
• Es veu també que la part reactiva augmenta amb la freqüència fins arribar lleugerament per sota del tram de circumferència corresponen als 0,2·50 = 10 Ω .
• A la figura es veu que el cursor es situa damunt de la freqüència central de 27.530 kHz .
• La gràfica evoluciona amb la freqüència en el sentit de les busques del rellotge.
Aquest comportament amb la freqüència ens indica la necessitat que els terminals d'una resistència siguin el més curts possible per a què aquesta es comporti com a tal quan treballa a freqüències prou elevades.
A continuació assajarem dos condensadors de 820 pF amb diferents longituds de terminals (fig. 9).
fig.9
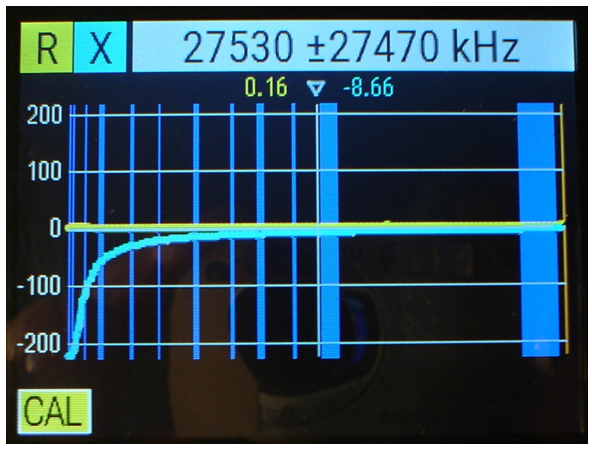
La fig. 10 ens indica el comportament del condensador de terminals curts amb la freqüència, en format RX, i observeu:
fig. 10
• Es veu com la reactància capacitiva va disminuint amb la freqüència i tendint a cero, com era d'esperar.
• El cursor, situat a la freqüència central de 27.530 kHz, indica que, a aquesta freqüència, la reactància del condensador val 8,66 Ω i la resistència equivalent de pèrdues en sèrie, 0,16 Ω . Desplaçant el cursor fins a la freqüència màxima de 55.000 kHz, ens indica un augment de la resistència de pèrdues de fins a més d'1 Ω .
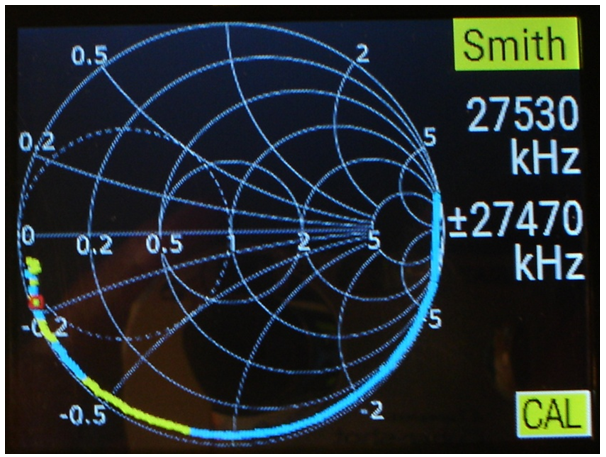
La fig. 11 ens indica el comportament del condensador en format carta de Smith, i observeu:
fig. 11
• A les freqüències més baixes el condensador es comporta gaire bé com un circuit obert.
• A la freqüència central, el cursor ens indica que la reactància capacitiva està per sota de 0,2·50 = 10 Ω , com hem vist abans en format RX . A freqüències superiors les pèrdues del condensador augmenten significativament.
• Aquí es veu clarament l'evolució de la gràfica en el sentit de les agulles del rellotge.
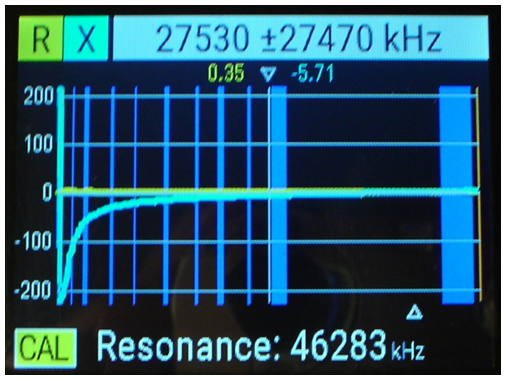
La fig.12 indica el comportament del condensador de terminals llargs en format RX, i observeu:
fig. 12
• Comparant aquesta gràfica amb la de la fig.10, l'analitzador ens indica una freqüència de ressonància sèrie a 46.283 kHz, la qual cosa es deu a la inductància en sèrie que afegeixen els terminals llargs i que ressona amb la capacitat del condensador a aquesta freqüència.
• Per aquest motiu la gràfica també ens indica que a la freqüència central de 27.530 kHz la reactància capacitiva val 5,71 Ω , valor inferior als 8,66 Ω anteriors, com era d'esperar -raoneu-ho.
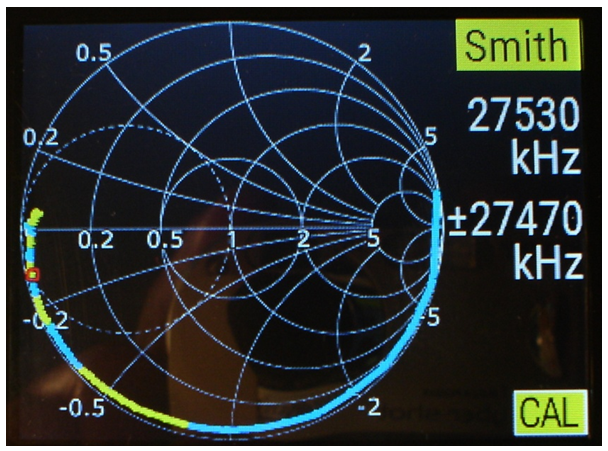
La fig.13 indica el comportament del condensador amb la freqüència en format carta de Smith, i observeu:
fig. 13
• La intersecció de la gràfica amb l'eix horitzontal -lloc geomètric de reactància nul·la- ens indica que hi ha ressonància sèrie. Desplaçant el cursor a aquest punt d'intersecció obtenim el valor de la freqüència de ressonància anterior.
• A freqüències superiors a la de ressonància predomina la reactància inductiva, llavors el condensador queda desvirtuat ja que es comporta com una bobina..
Igual que passa amb la resistència, cal que la longitud dels terminals d'un condensador sigui el més petita possible, per a que aquest es comporti com a tal quan treballa a freqüències prou elevades.
A continuació assagem una inductància de 0,47μH.
fig. 14
A la fig. 14 s'indica la inductància assajada, que és del tipus axial amb nucli de ferrita. A la fig.15 s'indica el seu comportament amb la freqüència en format RX , i observeu:
fig. 15
• Movent el cursor per prendre lectures a diverses freqüències, es constata que la reactància augmenta gaire bé linealment amb la freqüència i que la resistència sèrie equivalent de pèrdues -resistència del conductor i pèrdues en el nucli- no varia de forma significativa.
• A la freqüència central de 27.530 kHz, el cursor ens indica que la reactància inductiva val 79,73 Ω i la resistència total de pèrdues, 0,18 Ω .
La fig. 16 ens indica el comportament en format carta de Smith, i observeu:
fig. 16
• La gràfica arrenca pràcticament amb un curtcircuit i, degut a les baixes pèrdues de la bobina, recorre gaire bé la circumferència de resistència nul·la.
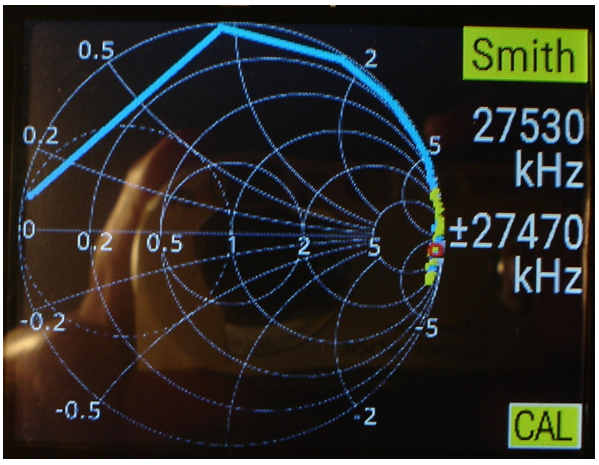
La fig. 17 ens indica el comportament en format carta de Smith d'una inductància de 22 μH del mateix tipus que l'anterior, i observeu:
fig. 17
• El seu major nombre d'espires fa que la capacitat paràsita total entre aquelles augmenti, amb la qual cosa presenta una freqüència d'autorresonància paral·lel que, a la vista de la posició del cursor, és inferior a la freqüència central de 27.530 kHz. Desplaçant el cursor es veu que aquesta freqüència està al voltant de 21.000 kHz .
• En aquest assaig s'observa que l'analitzador fa mesures discretes de freqüència i que en pantalla les presenta unides amb segments rectilinis.
Suggeriment: assageu components d'altres valors.