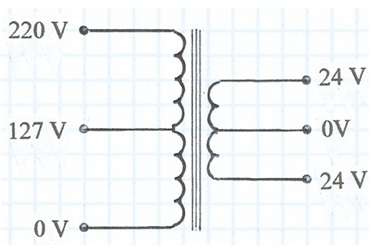
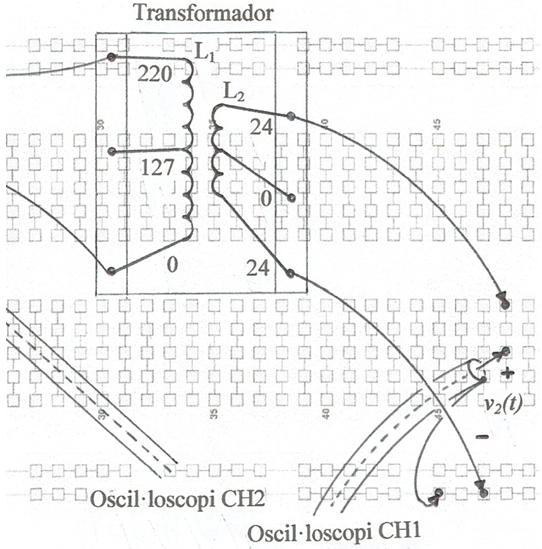
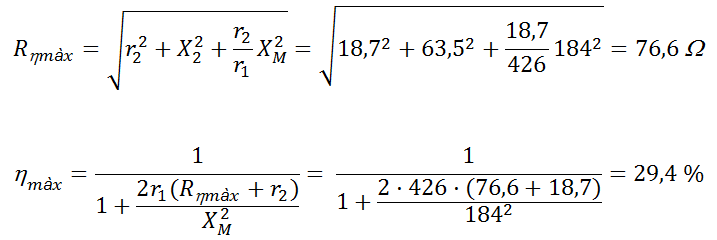Utilitzarem un petit transformador d'alimentació, del tipus obert, i li suprimirem el nucli ferromagnètic amb la qual cosa tindrem un transformador lineal -veure l'apèndix: El transformador lineal. Per exemple, a la fig. 1 s'indica el marcatge dels debanats d'un possible transformador a emprar.
fig. 1
Suprimir el nucli ferromagnètic té les seves dificultats; cal paciència i constància.
A la fig. 2 es pot veure el transformador sense el nucli. Se li han soldat uns terminals mascle per als cables que el connectaran a la protoboard.
fig. 2
A la fig. 3 es pot veure la preparació d'un dels cables. Per un extrem té un terminal femella per connectar-lo al transformador i per l'altre extrem un terminal mascle per inserir-lo a la protoboard.
fig. 3
Òbviament, es pot prescindir dels terminals femella i soldar els cables directament als terminals del transformador.
Assajarem el transformador emprant la totalitat dels debanats, és a dir, els terminals 0 V i 220 V per al primari i els terminals 24 V i 24 V per al secundari.
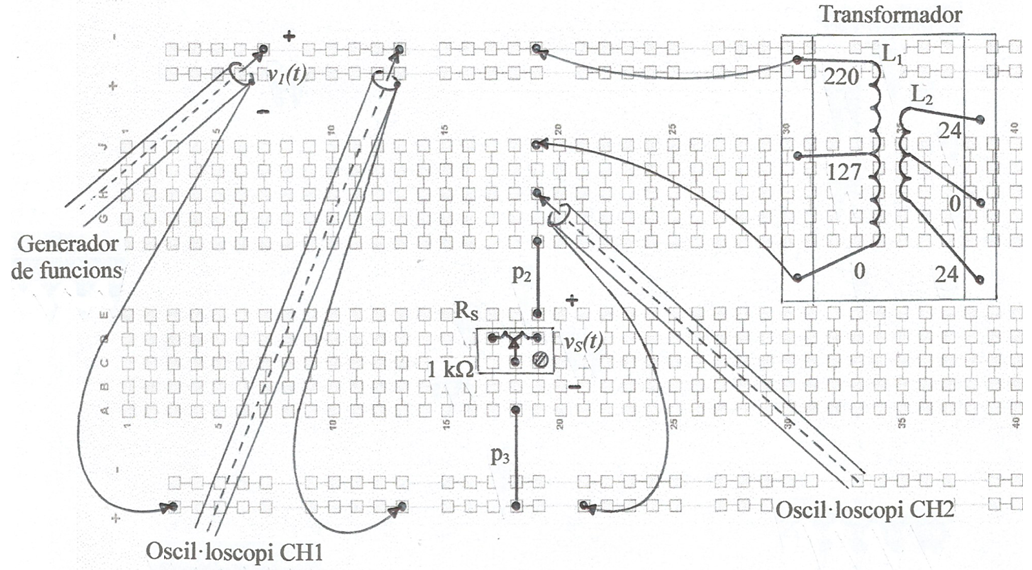
El primer que cal fer és determinar la freqüència d'autoressonància paral·lel fap del primari -veure la pràctica: Bobines. A la fig. 4 es recorda el circuit a utilitzar per fer-ho. El transformador està en buit. RS és una resistència sonda de corrent que ens permetrà veure a l'oscil·loscopi a quina freqüència v1(t) i i1(t) = vS(t) / RS estan en fase, la qual serà fap -raoneu-ho.
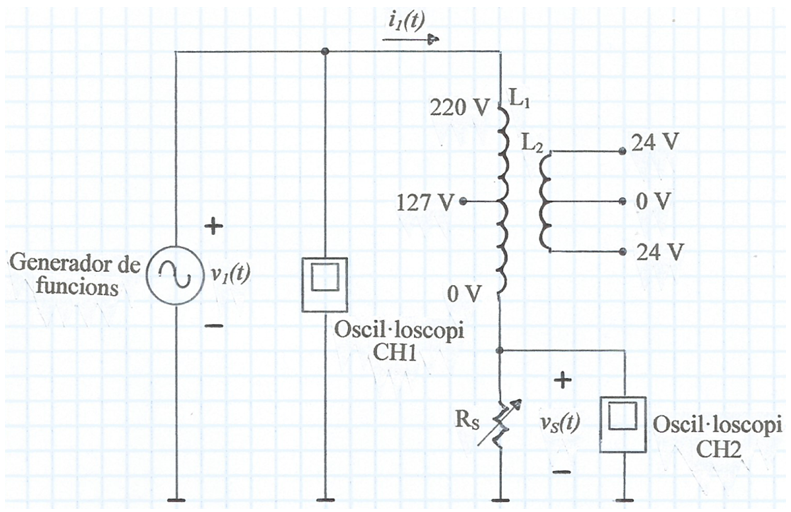
fig. 4
La relació de components i instruments per fer els assajos s'indica a continuació:
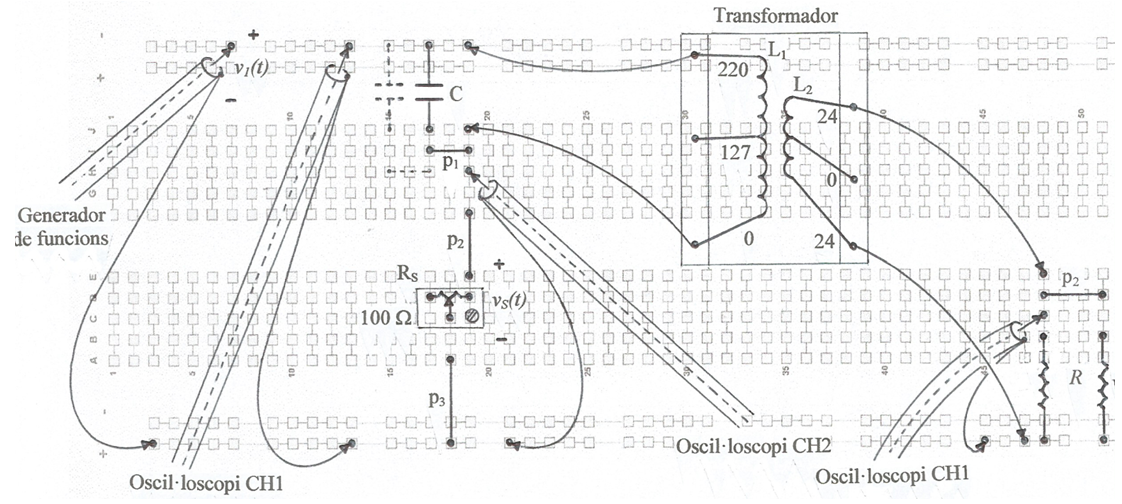
La planificació del muntatge a la protoboard s'indica a la fig. 5 i a la fig. 6, una fotografia.
fig. 5
fig. 6
Procediment:
• Amb el multímetre ajusteu el valor del potenciòmetre d'1 kΩ a uns 200 Ω , entre els terminals que s'utilitzen.
• En el generador de funcions seleccioneu la forma d'ona sinusoïdal.
• A una freqüència prou baixa, per exemple 500 Hz , comproveu que el corrent i1(t) està retardat respecte de la tensió v1(t) un angle 0 < φ < 90o , com correspon a una inductància i una resistència en sèrie; la del debanat més la sonda RS -raoneu-ho.
• Aneu augmentant la freqüència per comprovar que i1(t) va disminuint a la vegada que φ va tendint a 90o , com és d'esperar -raoneu-ho.
• Aneu augmentant més la freqüència i la sensibilitat del CH2 de l'oscil·loscopi fins comprovar que a la freqüència fap , passa:
1) La component fonamental del corrent passa per un valor mínim a conseqüència de l'efecte de filtre de rebuig de banda -raoneu-ho.
2) Queda en fase amb la tensió v1(t) .
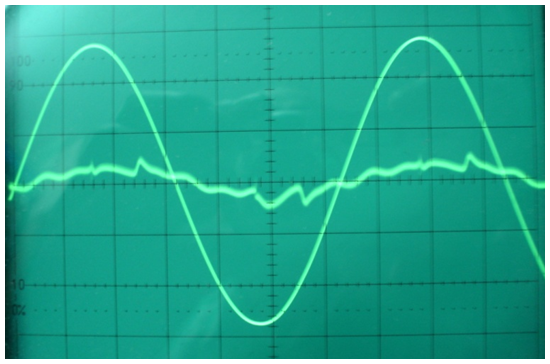
3) Superposats amb la fonamental apareixen els harmònics de la forma d'ona del corrent, la qual cosa ens diu que aquest no és exactament sinusoïdal -raoneu-ho. A la fig. 7 es poden veure les formes d'ona de la tensió i el corrent a la freqüència fap .
fig. 7
El valor de fap depèn del valor de la inductància del debanat, de la seva capacitat paràsita entre espires i de la capacitat paràsita entre espires del secundari reflectida al primari -raoneu-ho.
• Anoteu la fap que resulta ser, per exemple: ≅ 28,6 kHz .
• Gireu el transformador per alimentar-lo pel secundari entre els terminals extrems de 24 V i 24 V . Comproveu que la fap en aquestes condicions és sensiblement igual a la trobada abans. Això es deu a què, si bé la inductància d'aquest debanat és molt més petita que la del primari, la seva capacitat paràsita juntament amb la capacitat paràsita del primari reflectida al secundari, fan que ambdós valors de freqüència siguin pràcticament coincidents -raoneu tot això.
Un altre detall a observar és que la forma d'ona del corrent a la freqüència fap es manté pràcticament sinusoïdal, la qual cosa és deu a què, ara, la relació entre la inductància del debanat i la capacitat total en paral·lel és molt més petita, en conseqüència el factor de qualitat Q és molt més baix i l'efecte de filtre de rebuig de banda no és tan acusat com en el primari -raoneu-ho.
A continuació determinarem els paràmetres del transformador i ho farem a una freqüència molt per sota de la fap , per exemple 1 kHz , amb la qual cosa les capacitats paràsites dels debanats tindran un efecte menyspreable sobre les mesures -raoneu-ho.
Procediment:
• Amb el multímetre, mesureu la resistència r1 del primari i resulta, per exemple: r1 = 426 Ω
• Ajusteu la freqüència del senyal sinusoïdal a 1 kHz .
• Gireu de nou el transformador per alimentar-lo pel primari.
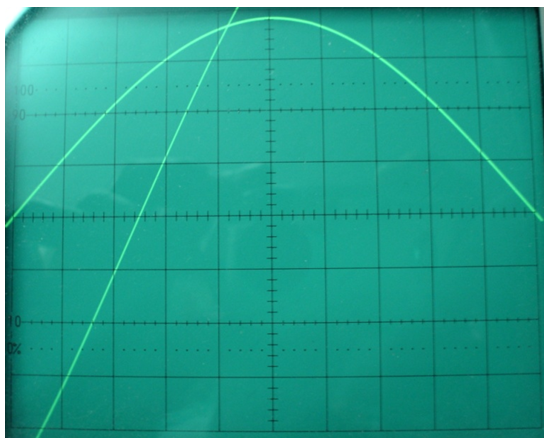
• Aneu augmentant el valor de RS fins que el retard del corrent respecte de la tensió aplicada sigui de 45o (fig. 8).
fig. 8
Observeu que expressament s'ha ajustat la sensibilitat del canal que mesura vS(t) = RS·i1(t) de manera que el senyal surti dels límits de la pantalla de l'oscil·loscopi, a fi que l'angle d'intersecció del senyal amb l'eix de temps sigui gran i poder així ajustar amb més precisió el desfasament de 45o .
• En aquesta condició de φ = 45o , la suma de la resistència r1 del primari més la resistència RS és igual a la reactància X1 d'aquest debanat -raoneu-ho.
• Amb el multímetre mesureu la resistència ajustada RS i surt, per exemple: RS = 470 Ω
llavors:
X1 = 426 + 470 = 896 Ω d'on L1 = X1 / ω = 896 / (2π·1000) = 142,6 mH
• Per contrastar aquests resultats podeu seguir el següent camí. A la fig. 8 la sensibilitat del canal que mesura la tensió v1(t) és d'1V/div , llavors, segons ens diu la pantalla de l'oscil·loscopi, el valor de pic d'aquesta és aproximadament de 3,82 V. Disminuint la sensibilitat del canal que mesura vS(t) per poder mesurar el seu valor de pic, aquest val, per exemple 1,45 V , llavors el valor de pic del corrent pel debanat val:
I1 = VS / RS = 1,45 V / 475,8 Ω = 3,047 mA
La magnitud de la impedància que "veu" la font val:
Z = V1 / I1 = 3,82 V / 3,047 mA = 1.253,7 Ω
llavors:
r1 + RS = X1 = Z / √2 = 1253,7 / √2 = 886,5 Ω i r1 = 886,5 - 470 = 416,5 Ω -raoneu-ho-
valors bastant semblants als trobats anteriorment. En aquesta segona determinació de X1 i de r1 intervenen més errors que en la primera -raoneu-ho- per la qual cosa sembla més raonable donar més crèdit als valors anteriors: X1 = 896 Ω i r1 = 426 Ω .
• Amb el CH1 de l'oscil·loscopi mesureu la tensió del secundari v2(t) entre els terminals extrems de 24 V i 24 V (fig. 9) .
fig.9
i resulta un valor de pic de, per exemple: V2 = 0,554 V , llavors la reactància mútua valdrà:
XM = V2 / I1 = 0,554 V / 3,047 mA = 181,82 Ω d'on LM = XM /ω = 181,82 / (2π·1000) = 28,94 mH
-raoneu tot això. Observeu l'avançament de 90o de v2(t) respecte de i1(t) -raoneu-ho.
• Ara gireu el transformador i l'alimenteu pel secundari entre els terminals extrems de 24V i 24 V i, seguint el mateix procediment que per al primari, mesurarem r2 amb el multímetre i determineu X2 emprant l'oscil·loscopi.
• La mesura de r2 resulta, per exemple: r2 = 18,7 Ω
• Emprant per a RS la resistència variable de 100 Ω , un cop ajustada resulta, per exemple: RS = 44,8 Ω , llavors:
X2 = 18,7 + 44,8 = 63,5 Ω d'on L2 = 63,5 / (2π·1000) = 10,1 mH
• Amb l'oscil·loscopi mesureu VS per poder calcular I2 i resulta, per exemple:
VS = 0,3 V d'on I2 = 0,3 V / 44,8 Ω = 6,696 mA
• Amb el CH1 de l'oscil·loscopi mesureu la tensió del primari entre els terminals extrems de 0 V i 220 V i surt, per exemple: V1 = 1,25 V , llavors podeu fer una altra determinació de la XM :
XM = V1 / I2 = 1,25 V / 6,696 mA = 186,7 Ω
que s'assembla bastant al trobat anteriorment. Fent la mitjana aritmètica d'ambdós valors:
XM = (181,2 + 186,7) / 2 = 184 Ω
d'on:
M = 184 / (2π·1000) = 29,28 mH i k = XM /√(X1X2) = 184 / √(896·63,5) = 0,77
-raoneu tot això.
• Les previsions de Rηmàx i ηmàx són, emprant les fórmules (20) i (21) obtingudes en l'apèndix: El transformador lineal :
• Per comprovar aquestes previsions preneu per a R , per exemple, dues resistències en paral·lel de valors nominals 82 Ω i 1500 Ω amb les quals s'obté un valor mesurat de 76,2 Ω , que és molt proper als 76,6 Ω calculats.
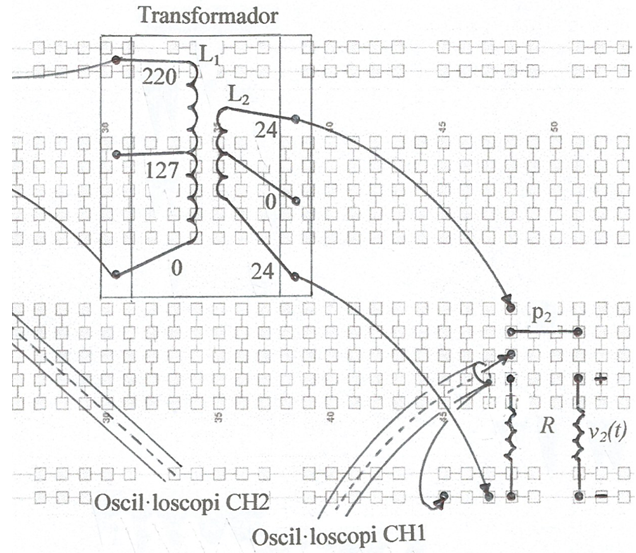
• Gireu de nou el transformador per alimentar-lo pel primari i carregeu el secundari amb la resistència de 76,2 Ω . A la fig. 10 s'indica la connexió d'aquesta càrrega al secundari.
fig. 10
• Per minimitzar errors i, a la vegada, facilitar el càlcul de la potència absorbida pel conjunt transformador-càrrega, es pot compensar el factor de potència mitjançant una capacitat C en sèrie, la reactància XC del qual sigui igual a la part imaginària de l'expressió (6) de l'apèndix: El transformador lineal, que es reprodueix a continuació -raoneu-ho.
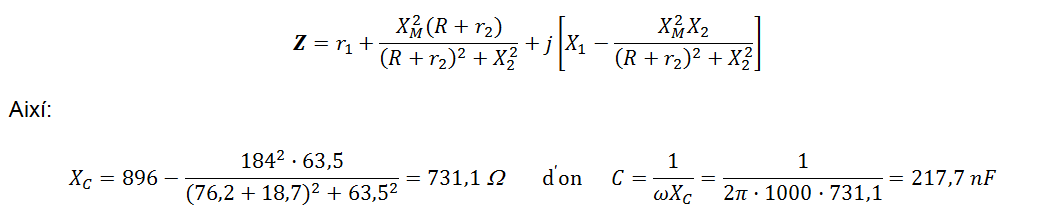
-raoneu-ho.
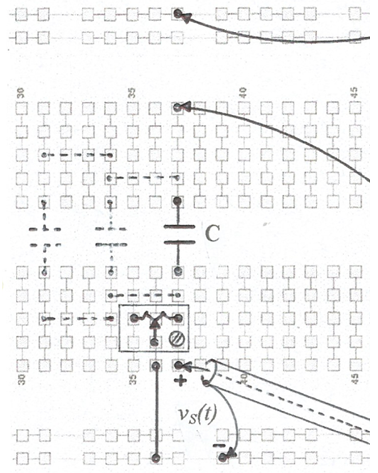
A la fig. 11 s'indica com inserir aquest condensador en el circuit. Probablement, provant amb alguns condensadors de valor nominal 220 nF en trobareu algun que s'ajusti bastant bé al valor que necessiteu i no caldrà combinar diversos condensadors. En cas necessari, a la figura i amb traç discontinu, s'indica com connectar alguns condensadors en paral·lel per aconseguir un valor el més ajustat possible. Amb el condensador correcte, v1(t) i i1(t) han d'estar pràcticament en fase.
fig. 11
• Ajusteu el nivell de sortida de la font a un valor còmode de llegir a la pantalla de l'oscil·loscopi; per exemple V1 = 3 V . Ajusteu la RS variable de 100 Ω aproximadament a la meitat del seu valor màxim, en un punt que permeti fer una lectura còmode de la tensió VS ; per exemple VS = 0,2 V .
• Amb el multímetre mesureu el valor ajustat de RS i resulta, per exemple: RS = 55 Ω , valor que permet calcular el corrent I1 pel primari:
I1 = VS / RS = 0,2 V / 55 Ω = 3,636 mA
i la potència PS dissipada per la sonda RS :
PS = RS · (I1/2)2 = 55 · (3,636·10-3/2)2 ·103 mW = 0,1817 mW
• Considerant que el condensador compensador és comporta pràcticament com un element sense pèrdues, la potència entregada per la font al conjunt transformador-càrrega i a la resistència RS val:
P1 = V1I1 cos 0o / 2 = 3 V · 3,636 mA / 2 = 5,454 mW -raoneu-ho-
i descomptant la potencia dissipada a la sonda RS tindrem la potència PT absorbida pel conjunt transformador-càrrega:
PT = P1 - PS = 5,454 - 0,1817 = 5,272 mW
• Amb el canal CH1 de l'oscil·loscopi mesureu la tensió en borns de la resistència de càrrega i resulta, per exemple: V2 = 0,464 V , llavors aquesta dissipa una potència:
P = V22 / (2R) = 0,4642 / (2·76,2) = 1,413 mW
• El rendiment η del transformador valdrà:
η = P / PT = 1,413 / 5,272 = 26,8 %
valor bastant semblant al previst. Si s'ha tingut força cura en fer les mesures, les diferències amb els valors previstos s'han d'atribuir principalment a errors dels instruments de mesura.
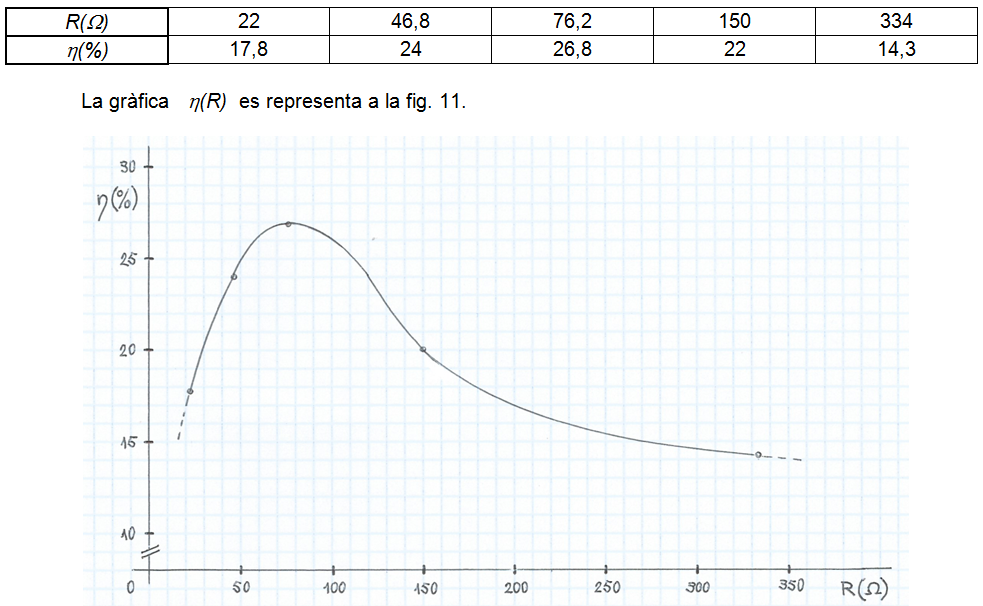
• Per comprovar que aquest rendiment és, efectivament, el màxim que es pot obtenir, assageu amb altres resistències de càrrega. Són adequats els valors nominals següents: 22 Ω , 47 Ω , 150 Ω i 330 Ω . Amb els valors reals de les resistències i els valors trobats de rendiment, feu la gràfica η(R) . A cada resistència de càrrega li correspon un valor de C per fer la compensació. Si no es fa la compensació, la potència P1 es pot calcular així: P1 = V1I1cosφ / 2 amb φ l'angle de retard de i1(t) respecte de v1(t) -raoneu-ho. Per exemple, s'ha obtingut la taula de valors següent:
fig. 11
Suggeriment: Feu un assaig a una freqüència més gran, per exemple 2 kHz -encara molt més baixa que la fap - per comprovar els augments de Rηmàx i de ηmàx i raoneu perquè augmenten.
Observació: Per fer la compensació del factor de potència amb un condensador en paral·lel amb el primari, s'ha de trobar l'admitància Y = 1 / Z que és:
A la fig. 13 s'indica com connectar condensadors en paral·lel amb el primari.
fig. 13
Comproveu que per a R = 76,2 Ω s'obté un C per compensar en paral·lel aproximadament de la meitat del valor del C per compensar en sèrie.