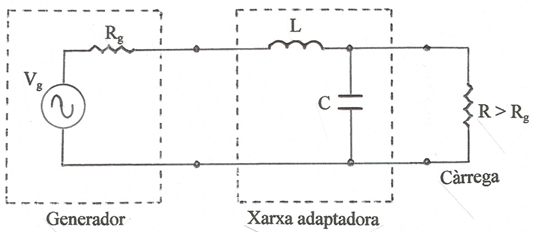
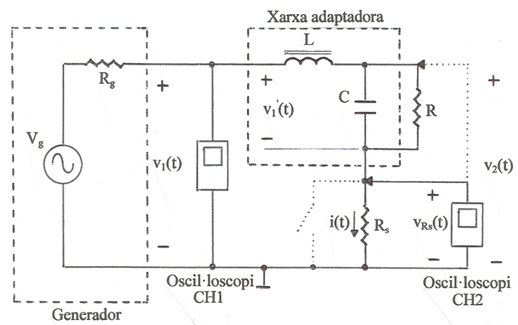
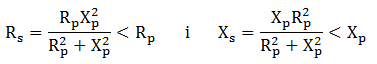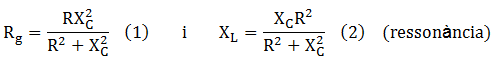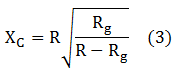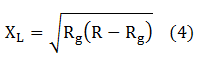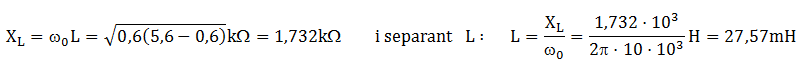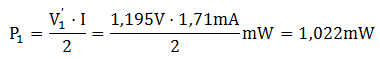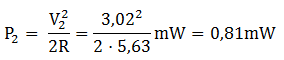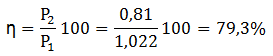Es pot donar el cas que una càrrega resistiva  R  hagi de treballar a una freqüència  f₀ ,  o en un marge estret de freqüències centrat a  f₀ , i la resistència interna  R_g  de la font on ha d'anar connectada sigui inferior a  R .  Per aconseguir la màxima transferència de potència de la font a la càrrega es pot emprar una xarxa adaptadora com la que es descriu a continuació.  A la fig. 1 s'indica l'esquemàtic i caldrà calcular els valors de  L  i de  C.  Per simplificar els càlculs considerarem que aquests elements reactius no tenen pèrdues.

fig. 1

             Recordatori:

            Per determinar els valors de  L  i de  C  comencem fent el circuit sèrie equivalent del paral·lel format per   R   i   −jX_C .

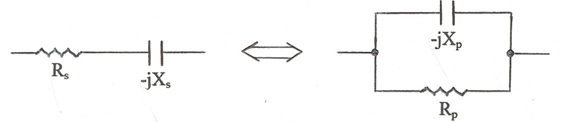
            Els circuits de la fig. 2 seran equivalents quan les seves immitàncies siguin iguals, la qual cosa ocorre a una determinada freqüència.

fig. 2

             Igualant impedàncies:

d'on:

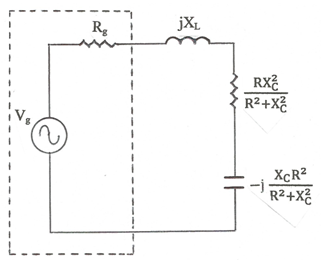
          A la fig. 3 es pot veure el circuit sèrie equivalent de la fig. 1.

fig. 3

           Per a que hi hagi adaptació s'haurà de complir:

           Separant  X_C  de  (1)  resulta:

i substituint  (3)  a  (2):

              Aplicació:

            Tenim una càrrega   R = 5,6 kΩ   que ha de treballar en règim permanent sinusoïdal, a una freqüència  f₀ = 10 kHz  i s'ha de connectar a una font de freqüència variable que té una resistència interna  R_g = 600 Ω. Calculeu els elements de la xarxa adaptadora en "L".

            Resolució:

            Com que  R > R_g  es pot emprar una xarxa com la descrita anteriorment.  Aplicant  (3):

            Aplicant  (4):

llavors utilitzarem els següents components de valors nominals: R = 5,6 kΩ ,  L = 27 mH  i  C = 8,2 nF.

            Per verificar el funcionament del la xarxa muntarem el circuit indicat a la fig. 4, on   R_s   és una resistència sonda que ens permetrà mesurar magnitud i fase del corrent   i(t)  pel circuit. El símbol de l'interruptor amb traç discontinu és en realitat un pont que permetrà curtcircuitar  R_s  quan calgui.  Amb l'oscil·loscopi es mesuraran els valors de pic de les tensions.

fig. 4

          Quan el circuit està ajustat a la freqüència correcta (freqüència de ressonància) ,  V₁  i  I  estaran en fase i es complirà  V₁^' = V₁ − V_Rs .  Per precisar més a l'hora de veure quan tensió i corrent estan en fase, es pot invertir momentàniament el CH2 per comprovar que les interseccions dels senyals es produeixen justament damunt de l'eix del temps.  R_s  pot ser de qualsevol valor, per exemple  47 Ω  de valor nominal.

            Les resistències són de  0,25 W  de dissipació.

            Relació de components:

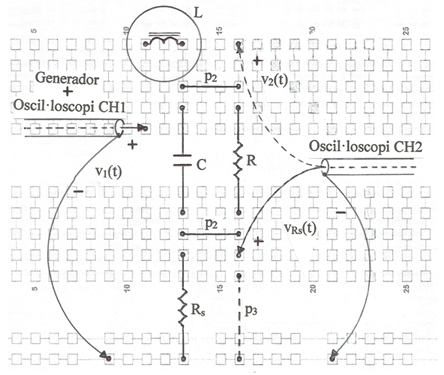
            La planificació del muntatge s'indica a la fig. 5 i a la fig. 6 una fotografia.

fig. 5

fig. 6

              Procediment:

            • Mesureu els valors reals de  R , R_s , L  i la seva resistència  r , C  i  R_g  i surten, per exemple:

 R = 5,63 kΩ      R_s = 46,8 Ω      L = 30 mH      r = 35,6 Ω     C = 8,32 nF    i    R_g = 646 Ω .  Per conèixer el valor de la resistència interna  R_g  del generador només cal carregar-lo amb una resistència variable -per exemple d'1 kΩ- i comprovar per a quin valor d'aquesta resistència el valor de la tensió cau fins a la meitat de la tensió en buit; en aquestes condicions el valor de la resistència variable coincideix amb el valor de  R_g (raoneu-ho). 

            • Sense el pont  p₃  es mesura  v_Rs(t) . Anoteu la freqüència a la qual  V₁  i  I  estan en fase i resulta, per exemple:  f₀ = 9.521 Hz 

            • Mesureu la tensió  V_Rs  que cau a  R_s  i surt, per exemple,  V_Rs = 80 mV  i calculeu el corrent  I:   I = 80 mV/46,8 Ω = 1,71 mA.

            • Mesureu  V₁  i calculeu   V₁^'  i surt, per exemple:  V₁ = 1,275 V   i   V₁^' = V₁ - V_Rs = 1275 - 80 = 1,195 V 

           • Calculeu la resistència reflectida  R^'  que "veu" la tensió  V₁^'  i surt, per exemple:  R^' = V₁^'/I = 1,195 V/1,75 mA = 682,9 Ω , valor que, com era d'esperar, ha de ser molt semblant al valor de  R_g però superior a ell, degut a la resistència equivalent en sèrie de pèrdues de la inductància, que s'hi afegeix.

            • Calculeu la potència  P₁ absorbida per  R  i la xarxa d'adaptació, i surt, per exemple:

           • Curtcircuiteu  R_s  amb el pont  p₃ , reajusteu  V₁  al valor anterior de  V₁^' = 1,195 V  i en el  CH2  de l'oscil·loscopi mesureu la tensió  V₂  en borns de  R,  i surt, per exemple:  V₂ = 3,02 V.

            • Calculeu la potència  P₂  absorbida per  R :

que, com era d'esperar, és inferior  a  P₁  degut a les pèrdues de la inductància -Cu i nucli.  Les pèrdues en el condensador es poden menystenir en front les pèrdues de la inductància. 

            • Finalment es pot calcular el rendiment de l'adaptació:

           Les diferències trobades respecte de les previsions teòriques són atribuïbles a les diferències entre els valors nominals i reals dels components. Si es vol reproduir la pràctica descrita i la font de senyal de que es disposa té una  R_g  diferent de  600 Ω, per exemple  R_g = 50 Ω ,  només cal connectar en sèrie amb la seva sortida una resistència de  600 - 50 = 550 Ω ,  valor que es pot aconseguir amb una resistència variable de, per exemple, 1 kΩ  o aproximadament amb una resistència fixa de  560 Ω  de valor nominal.

Escriure un comentari