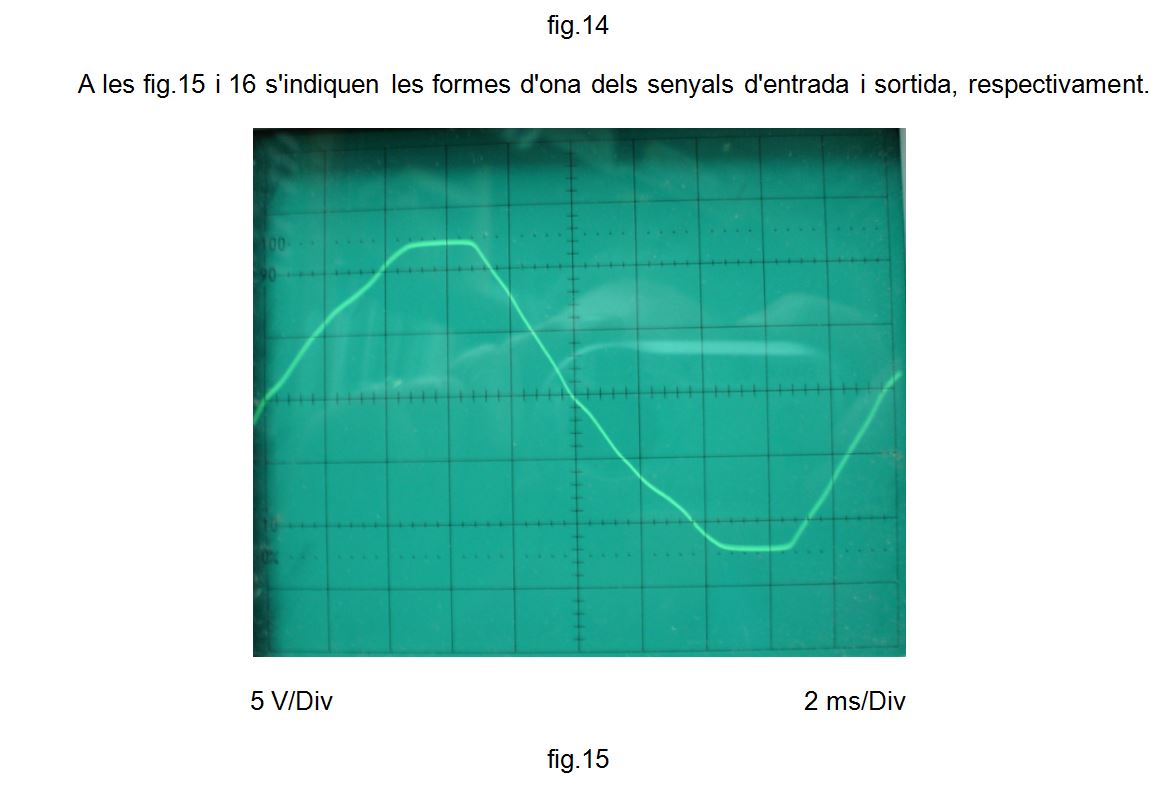
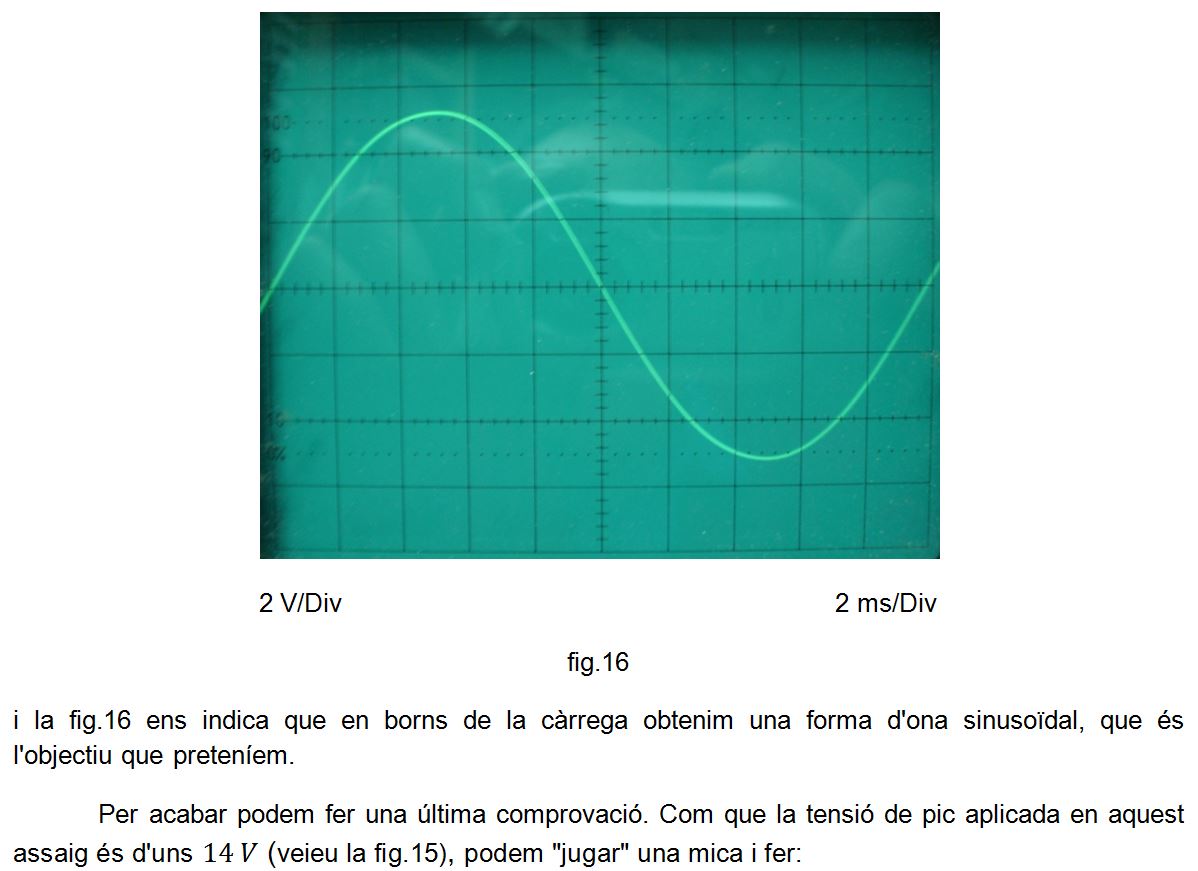
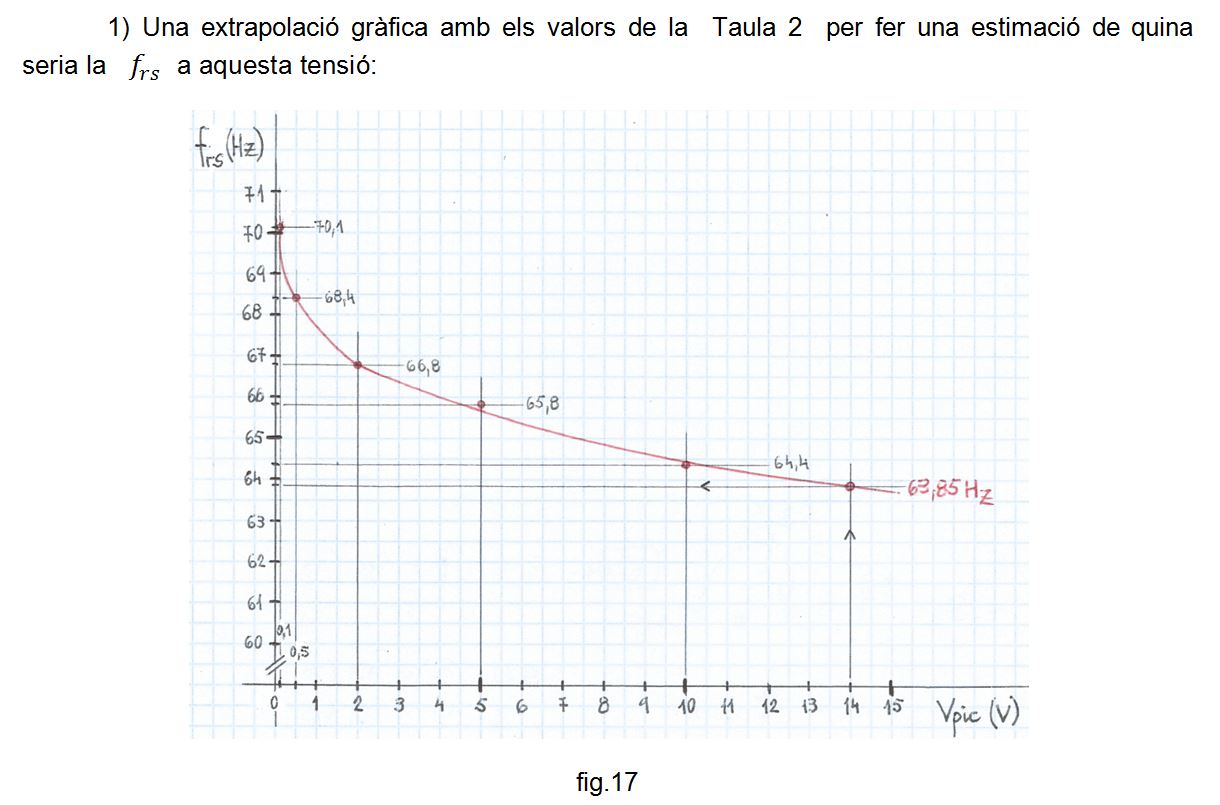
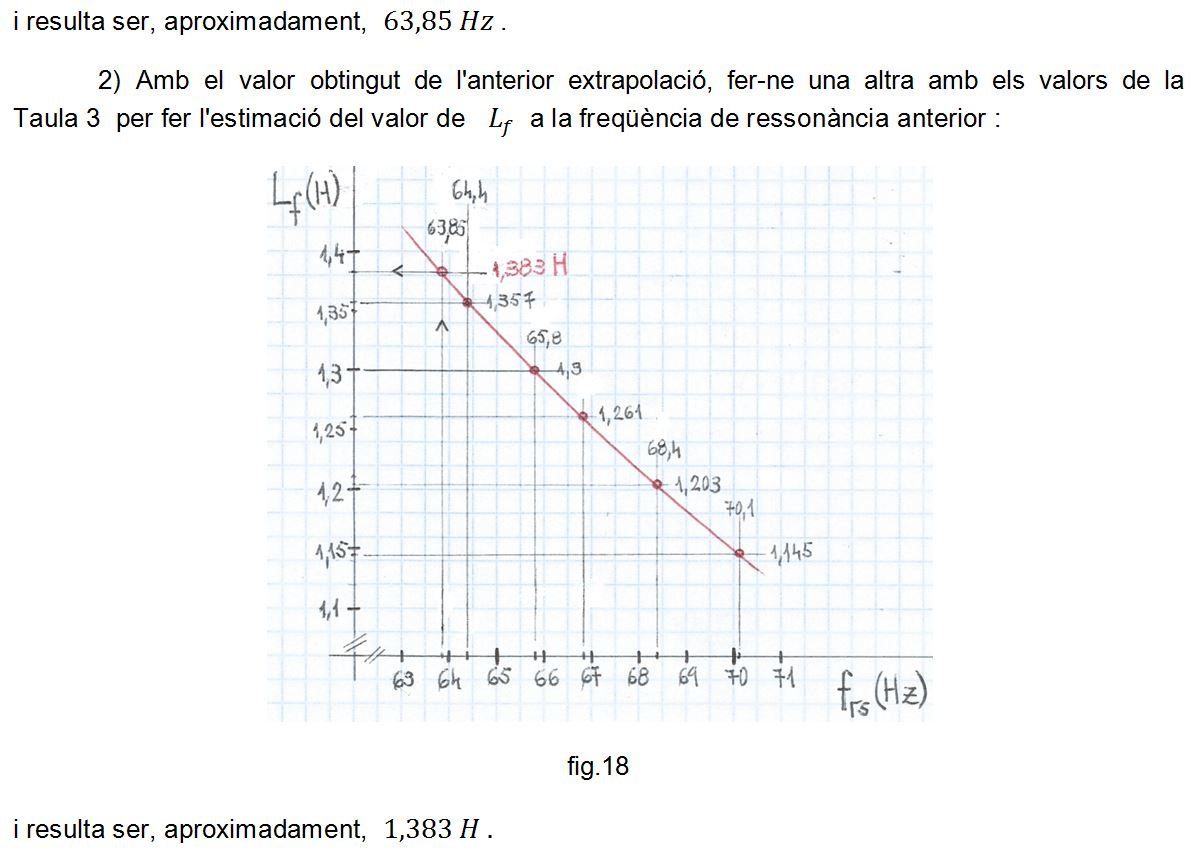
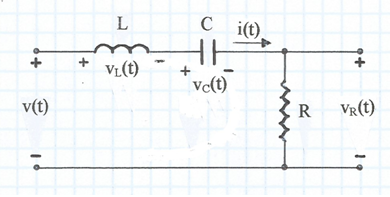
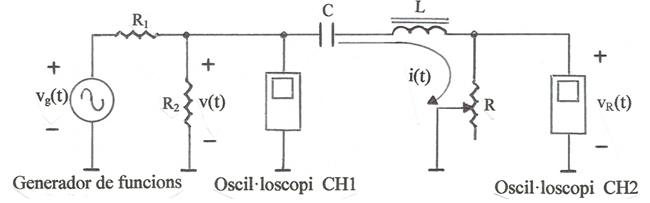
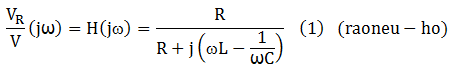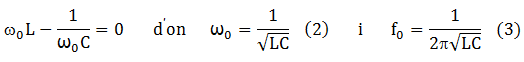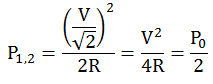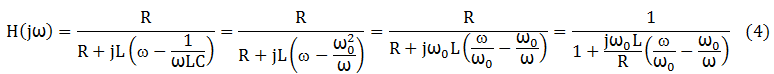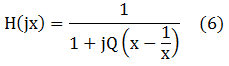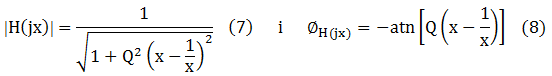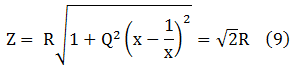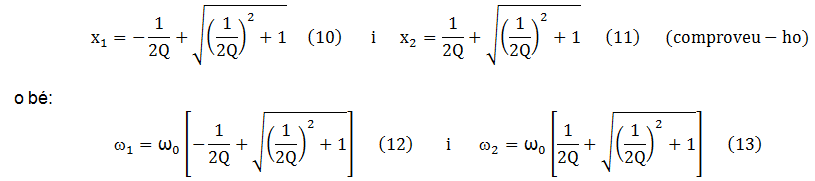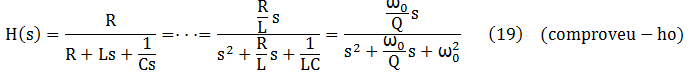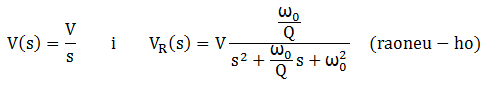A la fig. 1 s'indica l'esquemàtic.
fig. 1
R és la resistència sèrie total equivalent del circuit, és a dir, on s'hi inclouen: la resistència del conductor amb que s'ha construït la bobina, les pèrdues en el nucli -en el cas que en tingui-, les pèrdues en el dielèctric del condensador i qualsevol altra resistència afegida.
Recordatori:
La funció de transferència en règim permanent sinusoïdal VR(jω) / V(jω) , és:
Hi ha una freqüència ω0 , que se'n diu de ressonància, que anul·la la part imaginària del denominador de (1) i, en conseqüència, la funció de transferència val la unitat, és a dir, la tensió de sortida vR(t) està en fase i s'iguala amb la tensió d'entrada v(t) -raoneu-ho. La freqüència de ressonància ω0 val :
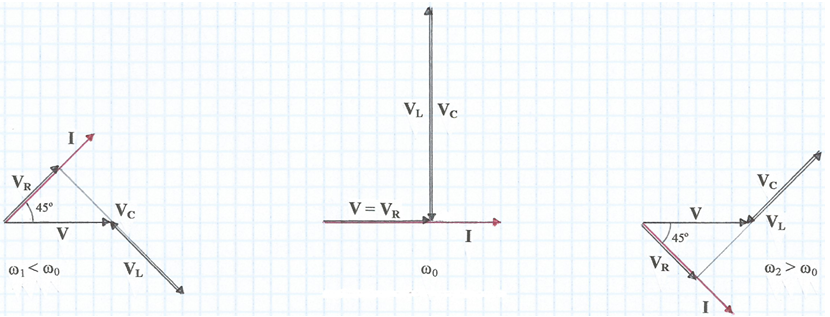
Hi haurà dues freqüències ω1 i ω2 , inferior i superior, respectivament, a ω0 per a les quals la magnitud de la fase serà de 45o, tal com s'indica en els diagrames fasorials de la fig. 2. A aquestes freqüències la magnitud de la reactància resultant és igual al valor de R -raoneu-ho.
fig. 2
Si l'amplitud V de la tensió aplicada al circuit es manté constant amb la freqüència, la tensió en borns de la resistència valdrà VR = V a ω0 i disminuirà fins VR = V/√2 a ω1 i ω2 -raoneu-ho. La potència dissipada per la R a ω0 val P0 = V2 / 2R -raoneu-ho- i la dissipada a ω1 i ω2 val :
Ara cal introduir ω0 a la (1) i ho podem fer de la següent manera :
per arribar finalment a l'expressió (4) que ens interessa -raoneu aquestes manipulacions.
Al quocient:
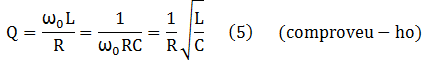
se'n diu factor de qualitat del circuit a la freqüència de ressonància ω0 -de seguida veurem perquè. Substituint (5) a (4) i dient x = ω/ω0 a la freqüència normalitzada respecte a la de ressonància, tenim:
La magnitud i la fase de (6) són, respectivament:
Per conveni, l'ampla de banda AB d'un filtre es defineix com la diferència de freqüències ω2 − ω1 per sobre i per sota de ω0 , respectivament, per a les quals la potència dissipada a R és la meitat que la dissipada a ω0 . Així, per determinar ω1 i ω2 només cal plantejar que a aquestes freqüències la magnitud de la impedància és √2 vegades el valor de R -raoneu-ho:
i separant x de (9) resulta:
Fent la diferència ω2 − ω1 i el producte ω1ω2 , s'obté :
La (15) ens dóna una altra manera d'expressar el Q i la (16) ens diu que f0 és la mitjana geomètrica de f1 i f2 .
Fent la diferència x2 - x1 i el producte x1x2 , s'obté :
A la inversa de Q també se'n diu ampla de banda relatiu -en relació a ω0 :
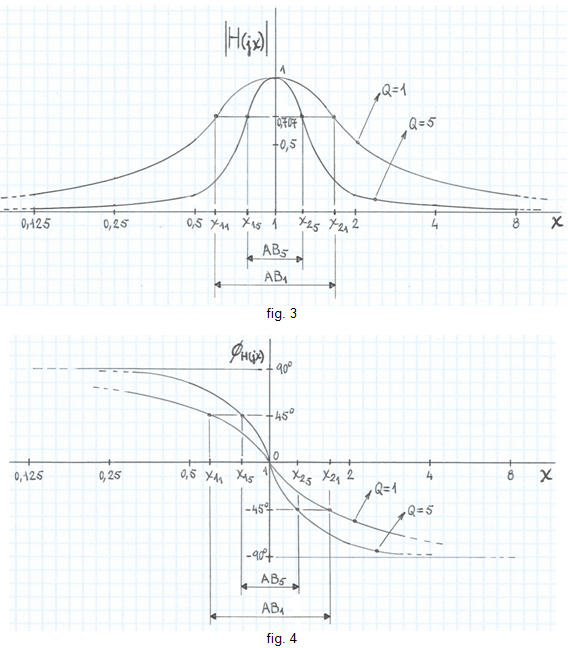
A les fig. 3 i 4 es representen (7) i (8), respectivament, per a dos valors de Q on es veu que com més gran és Q més 'punxeguda' es torna |H(jx)| i més gran és la magnitud del pendent de ØH(jx) al voltant de la freqüència de ressonància. AB1 = x21 - x11 és l'ampla de banda relatiu corresponent a Q = 1 i AB5 = x25 - x15 el corresponent a Q = 5 . El circuit actua, doncs, com un filtre passa-banda tant més selectiu com més alt és el Q , d'aquí el nom de factor de qualitat.
Expressant la (1) en el domini de la variable complexa s , tenim:
i a la (19) s'aprecia a simple vista l'estructura d'un filtre passa-banda on apareixen explícitament: 1) la freqüència de ressonància en el terme independent del denominador i 2) l'ampla de banda és el coeficient de la s .
Comparant el coeficient de la s de (19) amb la seva forma normalitzada 2ξω0 , trobem la relació entre ξ i Q :
A la fig. 5 s'indica l'esquemàtic del circuit a assajar.
fig. 5
La tensió v(t) aplicada al circuit prové d'un divisor de tensió connectat a la sortida del generador de funcions, on R2 és molt més petita que R1 a fi que les variacions de corrent de i(t) amb la freqüència afectin poc a la forma d'ona de v(t) (raoneu-ho). En conseqüència, el nivell de sortida del generador de funcions s'haurà d'ajustar gaire bé al màxim.
Relació de components:
Les resistències són de 0,25 W de dissipació.
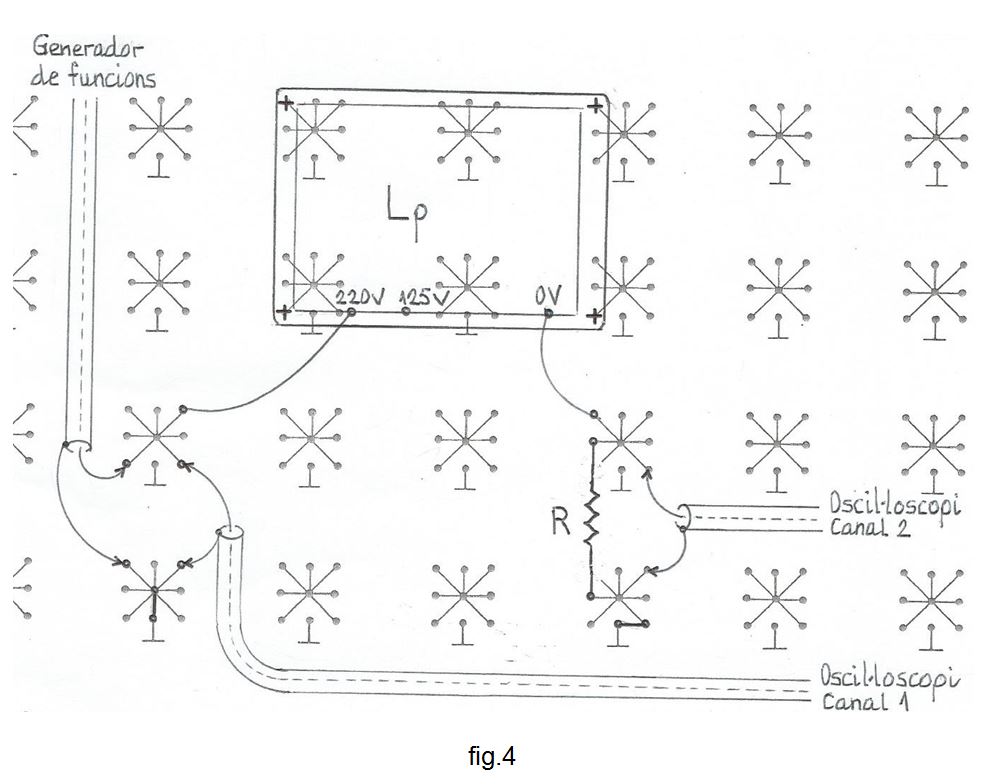
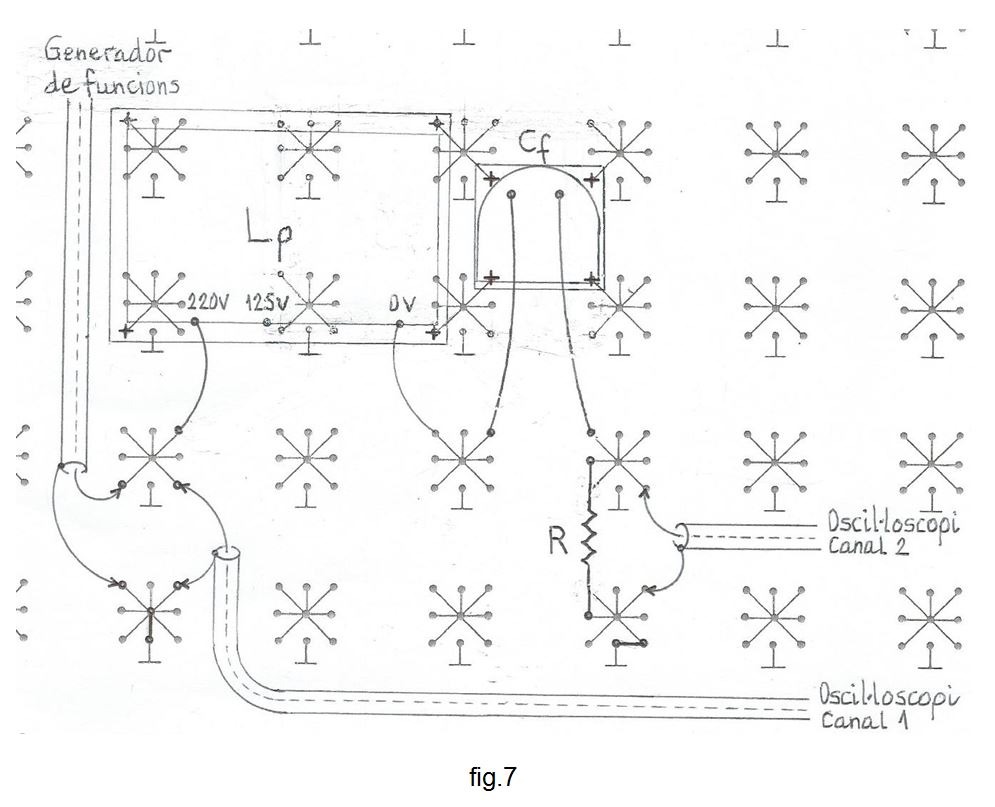
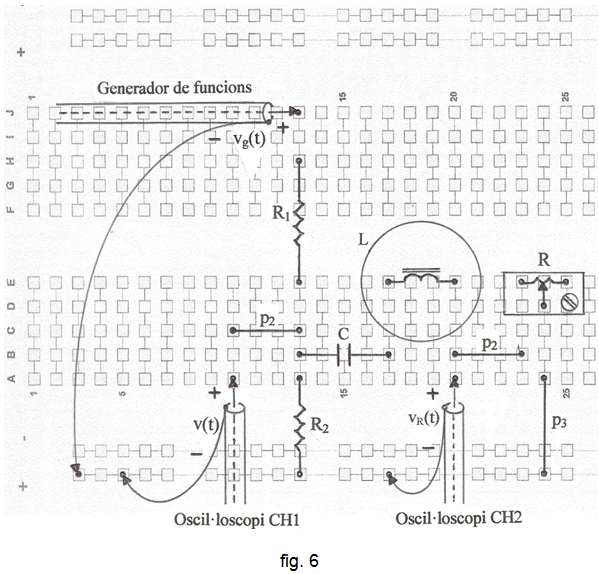
La planificació del muntatge s'indica a la fig. 6 i a la fig. 7, una fotografia.
Recordatori:
Si la tensió aplicada és un esglaó d'amplitud V, llavors:
i la vR(t) serà una exponencial decreixent si el valor de Q és baix, o serà una oscil·lació amortida si Q és alt. Per poder visualitzar a l'oscil·loscopi la forma dels transitoris de vR(t) quan v(t) és un esglaó, es seleccionarà un senyal periòdic rectangular el semiperíode del qual sigui suficientment gran per poder veure'ls completament.
Procediment i suggeriments:
• Mesureu els valors reals del condensador i de la inductància i la seva resistència.
• Ajusteu la resistència variable al seu valor màxim i mesureu-lo.
• Al generador de funcions seleccioneu forma d'ona rectangular, una freqüència d'uns 200 Hz i el nivell de sortida gaire bé al màxim.
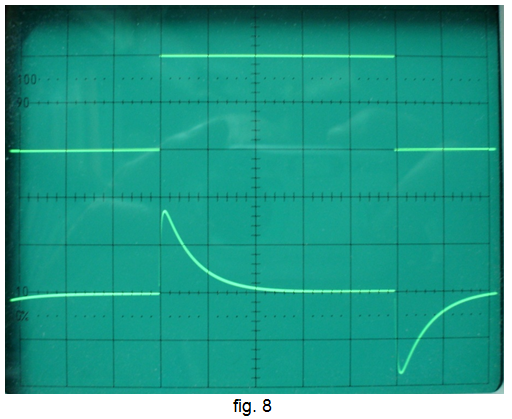
• Seleccioneu una base de temps de 0,5 ms/div , ajusteu les sensibilitats dels canals adequadament per poder veure els senyals i separar-los, tal com s'indica a la fig. 8. El senyal de sortida a d'estar sobreamortit. Comproveu si aquest senyal està d'acord amb les previsions que s'hagin pogut fer.
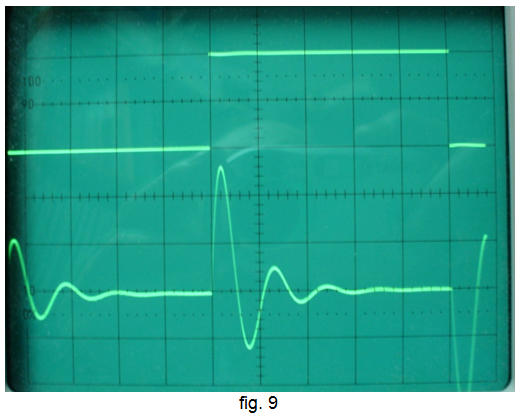
•Disminuïu el valor de la resistència variable fins uns 600 Ω per visualitzar una resposta subamortida, tal com s'indica a la fig. 9. Al disminuir el valor de R es veurà que s'ha d'augmentar la sensibilitat del canal per poder visualitzar bé el senyal.
• Aneu augmentant el valor de R per veure com es produeix la transició de subamortiment a sobreamortiment, passant per l'amortiment crític. Aneu ajustant la sensibilitat del canal segons convingui.
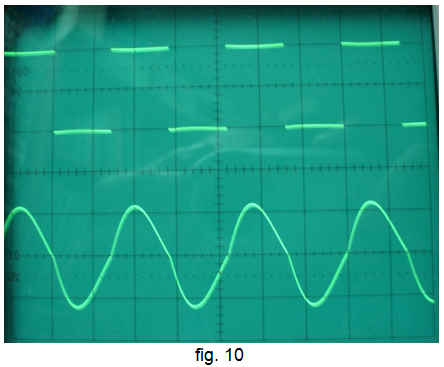
• Partint d'una situació de subamortiment, augmenteu la freqüència per mesurar la de ressonància, és a dir, la freqüència a la qual s'obté un senyal de sortida gaire bé sinusoïdal, d'amplitud màxima, tal com s'indica a la fig. 10. Interpreteu el fet que com més petit és el valor de R , apart de que l'amplitud del senyal disminueix, la forma d'ona s'acosta més a la sinusoide perfecte.
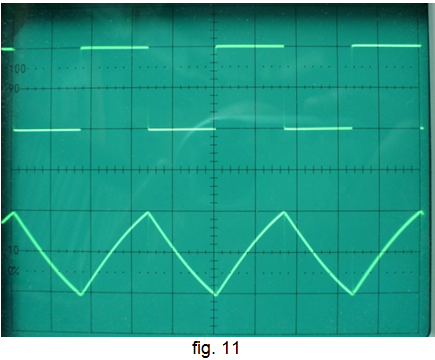
• Augmenteu la freqüència fins uns 6 kHz i interpreteu la forma del senyal de sortida (fig. 11).
• Seleccioneu forma d'ona sinusoïdal per a què el circuit treballi en règim permanent sinusoïdal. Ajusteu el valor de R de manera que el sistema estigui subamortit. Superposeu els senyals a la pantalla de l'oscil·loscopi i comproveu el valor de la freqüència de ressonància:
i comproveu si està d'acord amb el valor previst. Per a f = f0 el senyal de sortida passa per un màxim i està en fase amb el senyal d'entrada.
Observació: el valor de pic de vR(t) serà inferior al valor de pic de v(t) ja que no estem mesurant la caiguda de tensió corresponent a les pèrdues equivalents en sèrie dels components, principalment la caiguda de tensió en la resistència del conductor amb que s'ha construït la bobina -raoneu-ho.
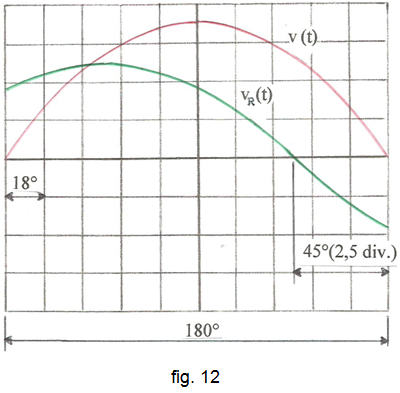
• Mesureu la freqüència f1 per sota de la f0 per a la qual el senyal de sortida vR(t) = Ri(t) està avançat un angle de 45o respecte del senyal d'entrada v(t) . A la fig. 12 s'indica com mesurar aquest desfasament amb l'oscil·loscopi, ajustant els senyals a la pantalla mirant d'aprofitar al màxim la resolució que aquesta ens proporciona.
• Utilitzant el mateix procediment anterior, mesureu la freqüència f2 per sobre de la f0 per a la qual el senyal de sortida està retardat un angle de 45o respecte del senyal d'entrada. Apliqueu la (15) per calcular el Q realment obtingut i compareu-lo amb el previst segons els valors dels components.
• Assageu altres valors de L i de C .