Aquest article va dirigit a qui estigui interessat en la Radioafició.
Abans de fer aquesta pràctica cal haver fet, o al menys llegit, l'anterior : Analitzador de xarxes. Comportament de resistències, capacitats i inductàncies amb la freqüència.
Si tenim una antena que ressona en una determinada freqüència f , la seva impedància serà resistiva i d'un valor que n'hi direm R , el qual dependrà, principalment, del tipus d'antena i del punt d'alimentació. Si aquesta antena s'ha de connectar a un emissor, la impedància de sortida del qual és també resistiva i de valor r ≠ R , una opció és intercalar una xarxa adaptadora d'impedàncies (acoblador) a fi d'obtenir la màxima transferència de potència de l'emissor a l'antena i, a la vegada, protegir l'emissor de possibles escalfaments excessius que pot produir la potència reflectida per manca d'adaptació.
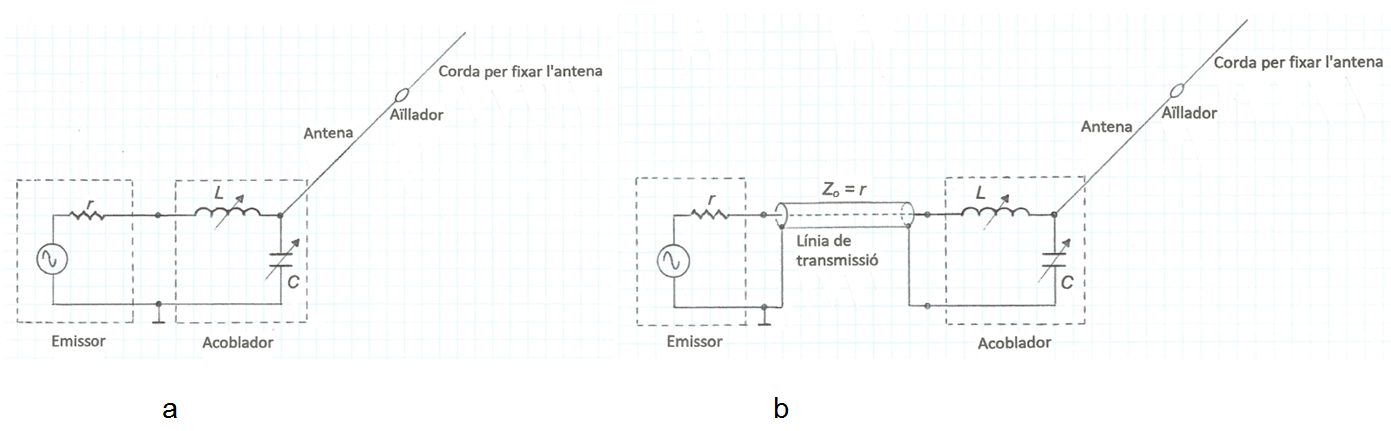
A la fig. 1 s'indiquen, entre d'altres, dues situacions on es pot emprar aquest senzill d'acoblador.
fig. 1
Es representa el circuit equivalent de sortida de l'emissor mitjançant una font de tensió en sèrie amb una resistència interna r -model Thevenin. A la fig.1a l'acoblador es connecta directament a la sortida de l'emissor. A la fig. 1b hi ha un tram de línia de transmissió d'impedància característica igual a la resistència interna de l'emissor (Zo = r) , que connecta l'emissor amb l'acoblador. En ambdós casos l'antena consisteix simplement en un conductor la longitud del qual sigui ressonant a la freqüència d'interès. Amb una anàlisi més general d'aquesta xarxa d'acoblament es pot demostrar que la longitud del conductor pot ser qualsevol, és a dir, una antena no ressonant, sempre que la L i el C siguin dels valors adequats per compensar la part reactiva de l'antena.
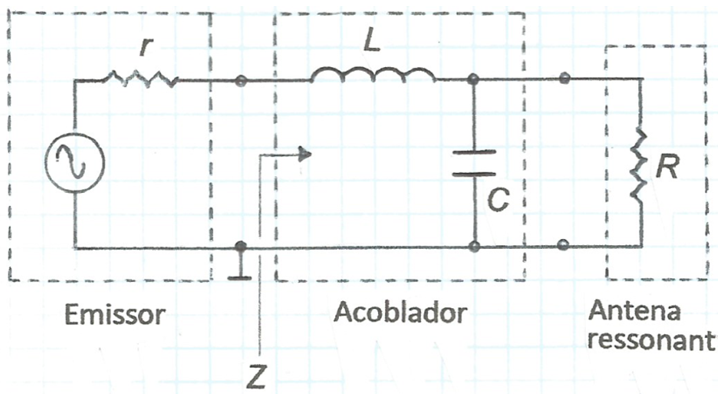
La xarxa que ja hem vist en anteriors articles i que analitzarem de nou, és la que s'indica novament a la fig. 2 .
fig. 2
La impedància Z en borns del conjunt acoblador-antena val :
i el parell d'equacions (6) i (7) ens donen els valors de les reactàncies que ens permetran fer l'adaptació d'impedàncies desitjada. Cal observar que aquestes equacions només es poden aplicar en els casos que R > r . Les fórmules ens diuen que si fos R = r llavors XL = 0 (L = 0) i XC = ∞ (C = 0) , és a dir, no caldria xarxa adaptadora, com era d'esperar.
Per exemple, si r = 50 Ω , que és un valor normalitzat per a la impedància de sortida dels equips de comunicacions, i es disposa d'una antena ressonant a f = 3,5 MHz la impedància de la qual val, per exemple, R = 437 Ω , els valors de L i de C hauran de ser :

fig. 3
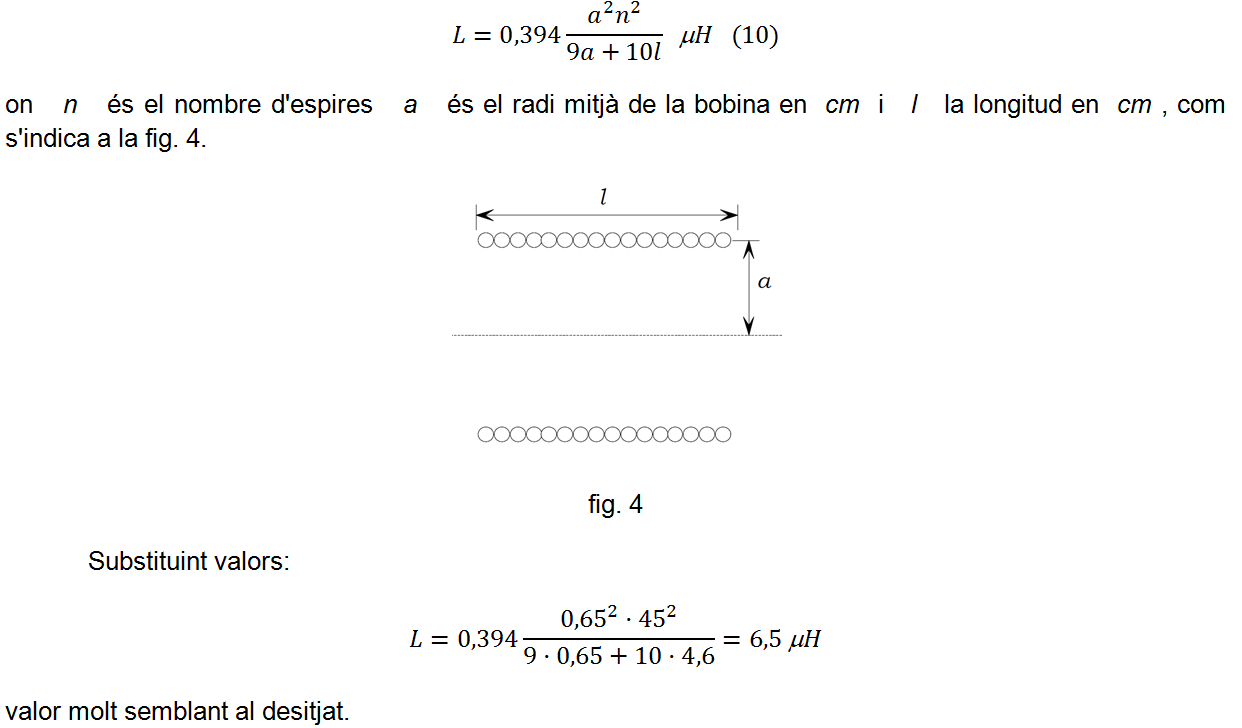
És un rodet de 12 mm de diàmetre exterior on es bobinen n = 45 espires, juntes, de fil de Cu esmaltat d' 1 mm de diàmetre, amb la qual cosa resulta un debanat d'uns l = 46 mm de longitud. Com es veu a la figura, als terminals de la L s'hi han soldat conductors flexibles acabats amb uns trossets de conductors rígids de 0,8 mm de diàmetre a fi d'assegurar bons contactes amb els nodes de la protoboard. El valor aproximat de la inductància d'aquesta bobina es pot calcular per la fórmula de Wheeler :
A continuació, amb l'analitzador cal comprovar el valor real de la inductància i també, degut a la capacitat paràsita entre espires que tota bobina presenta, el marge de freqüències per al qual la inductància es comporta com a tal.
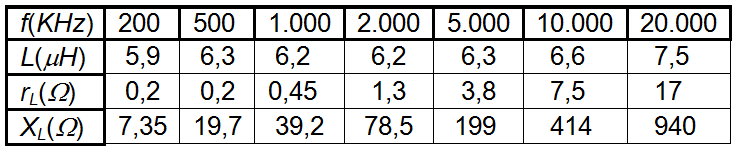
Després de fer la calibració prèvia de l'analitzador -com s'indica a l'anterior article: Analitzador de xarxes. Comportament de resistències, capacitats i inductàncies amb la freqüència - les mesures són, per exemple :
on es veu que el valor de la inductància és molt semblant al previst i que la bobina es comporta com a tal fins a uns 10 MHz . XL és el valor de la reactància inductiva la qual augmenta linealment amb la freqüència i rL és la resistència en sèrie equivalent de les pèrdues de la bobina la qual presenta un augment no lineal amb al freqüència.
Quan al condensador, se n'utilitza un de variable de 420 pF com l'indicat a la fig. 5. Igual que per a la bobina, se li han soldat cables als terminals per poder inserir-lo a la protoboard. També es pot veure a la figura una petita base de placa perforada de fibra de vidre, amb terminals, per poder fixar-lo mínimament a la protoboard, així com un botó de comandament .
fig. 5
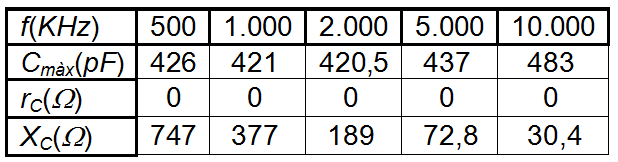
Igual com s'ha fet amb la bobina, cal comprovar prèviament el marge de freqüències per al qual el condensador es comporta com a tal, ja que les longituds dels terminals introdueixen inductàncies paràsites. Les mesures amb el condensador tot tancat -màxima capacitat- són, per exemple :
on es veu que el condensador es comporta com a tal fins a uns 5 MHz. XC és la reactància capacitiva que disminueix inversament amb al freqüència i rC és la resistència en sèrie equivalent de pèrdues que, com es veu, és pràcticament nul·la, la qual cosa es deu a que el dielèctric del C és aire.
La impedància resistiva de 437 Ω de l'antena s'implementa amb dues resistències de pel·lícula de grafit de 390 Ω i 47 Ω en sèrie.
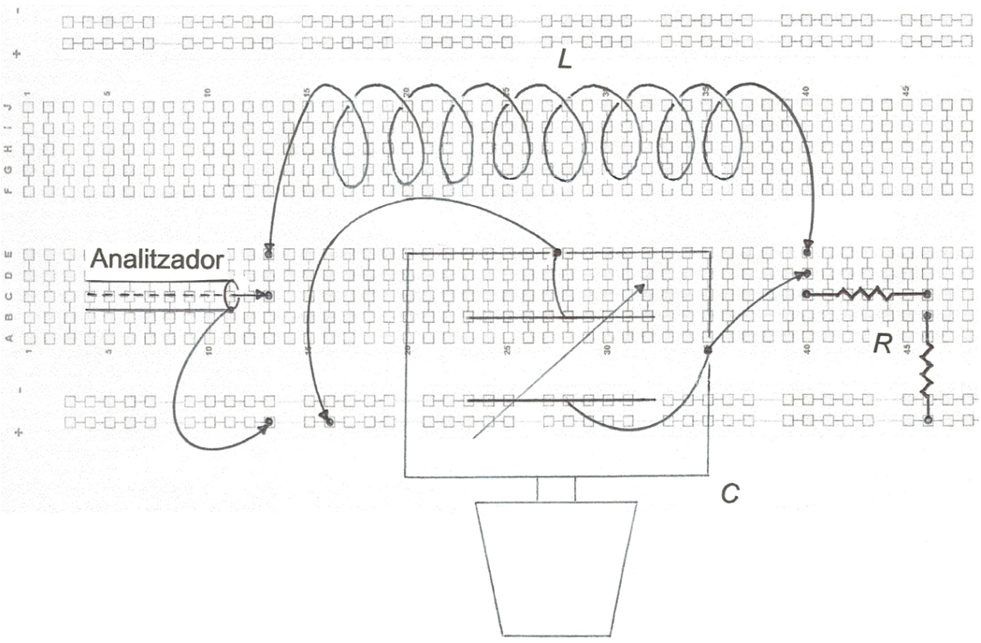
La planificació del muntatge a la protoboard s'indica a la fig. 6 i a la fig. 7, una fotografia.
fig. 6
fig. 7
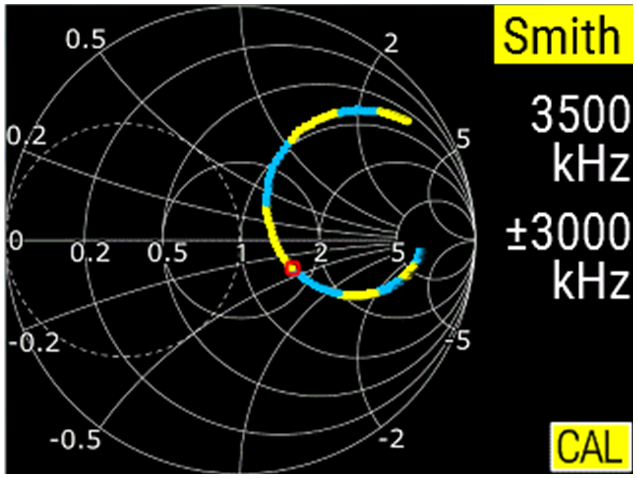
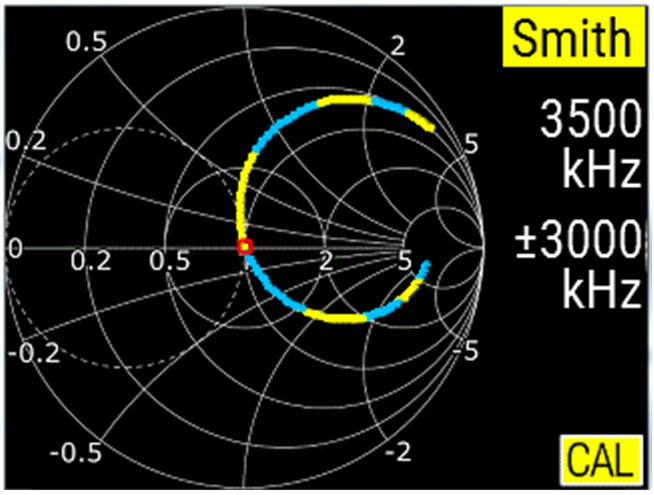
La carta d'Smith de la fig. 8 està normalitzada a 50 Ω per la qual cosa el seu centre correspon a una impedància de 50 + j0 Ω . Emprant aquest format, si fixem la freqüència central als 3,5 MHz que ens interessen i uns marges de, per exemple, ± 3 MHz, és a dir, unes freqüències mínima i màxima de 0,5 MHz i 6,5 MHz , respectivament, la posició del cursor -quadradet vermell- ens indicarà quan l'adaptació és correcta.
La imatge de la fig. 8 ens diu que s'ha de tancar més el condensador variable ja que en aquesta posició el valor de la capacitat és insuficient.
fig. 8
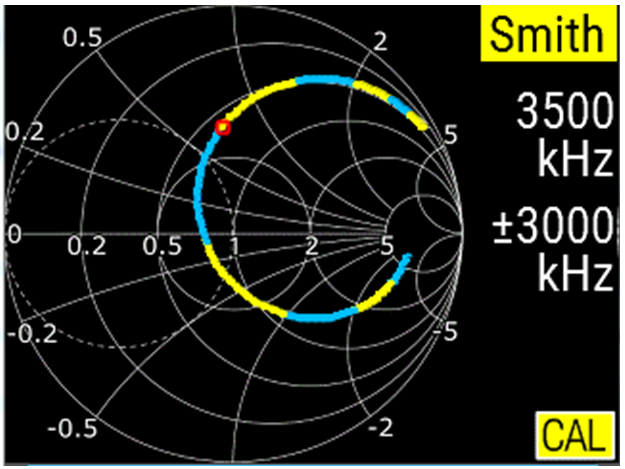
La imatge de la fig. 9 ens diu que s'ha d'obrir més el condensador ja que la capacitat és excessiva.
fig. 9
La imatge de la fig. 10 ens diu que la posició del condensador és l'adequada ja que el cursor queda justament en el mig de la carta, el què ens indica una adaptació correcta.
fig. 10
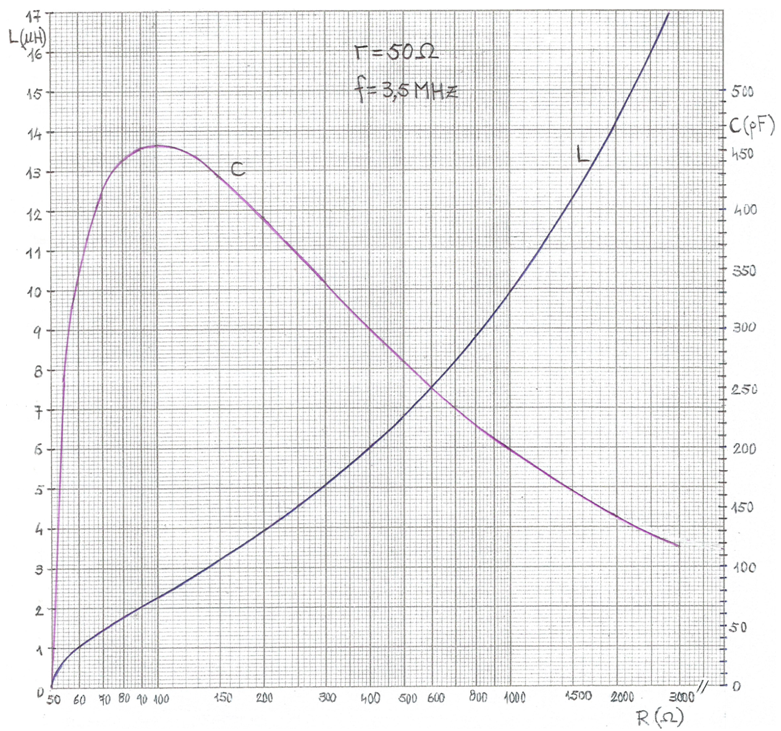
Observació: L'eix d'abscisses s'ha graduat a escala logarítmica per poder emprar les gràfiques fins a impedàncies d'antenes ressonants tan altes com 3.000 Ω .
fig. 13
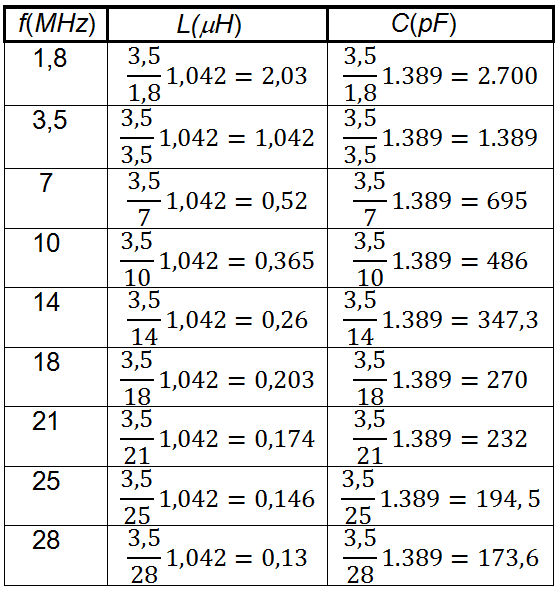
Com que els valors de L i C són inversament proporcionals a la freqüència, per trobar aquests valors a altres freqüències només cal aplicar aquesta proporció inversa. A la següent taula de valors s'indiquen, per a R = 437 Ω , els valors de L i C a les freqüències de 1,8 MHz, 3,5 MHz, 7 MHz, 10 MHz, 14 MHz, 18 MHz, 21 MHz, 25 MHz i 28 MHz . En definitiva, el parell de gràfiques de la fig. 3 i la taula són suficients per determinar els valors de L i C per a qualssevol valors de R i de f .
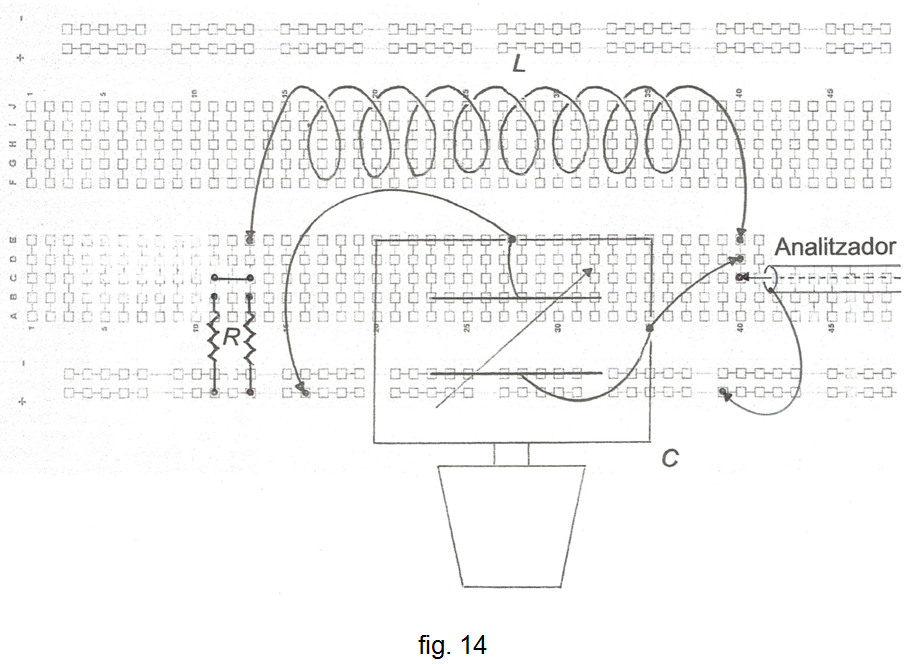
Observació: Com a comprovació final, suprimiu les resistències, connecteu en el seu lloc l'analitzador i on abans hi havia aquest connectat, connecteu-hi dues resistències de 100 Ω en paral·lel a fi d'obtenir una càrrega de 50 Ω , com s'indica a la fig. 14.
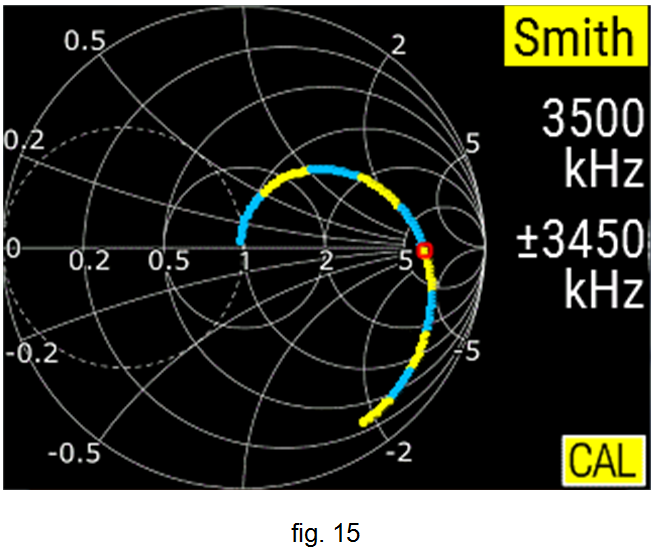
En format de carta d'Smith ara s'ha de veure l'adaptació inversa, és a dir, una transformació d'impedàncies de 50 + j0 Ω a 437 + j0 Ω com s'indica a la fig. 15. S'observa que, en aquest cas, amb la carta d'Smith ens manca precisió per poder llegir valors elevats d'impedàncies.
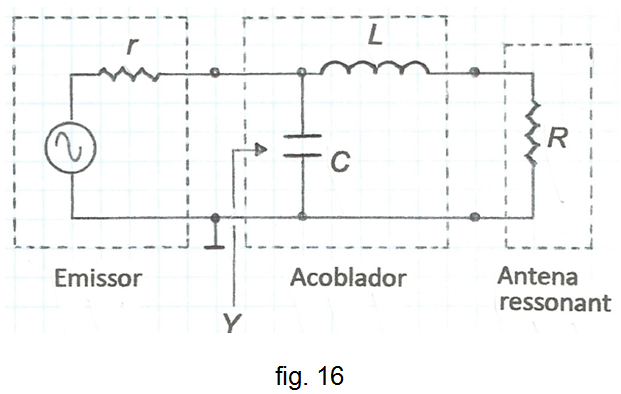
Així, en els casos que R < r es pot emprar la mateixa xarxa però invertint-la. A la fig. 16 s'indica aquest situació.
Si comparem (16) i (17) amb (6) i (7), es veu que són les mateixes fórmules on s'han intercanviat els papers de r i R , llavors només es poden aplicar quan r > R .
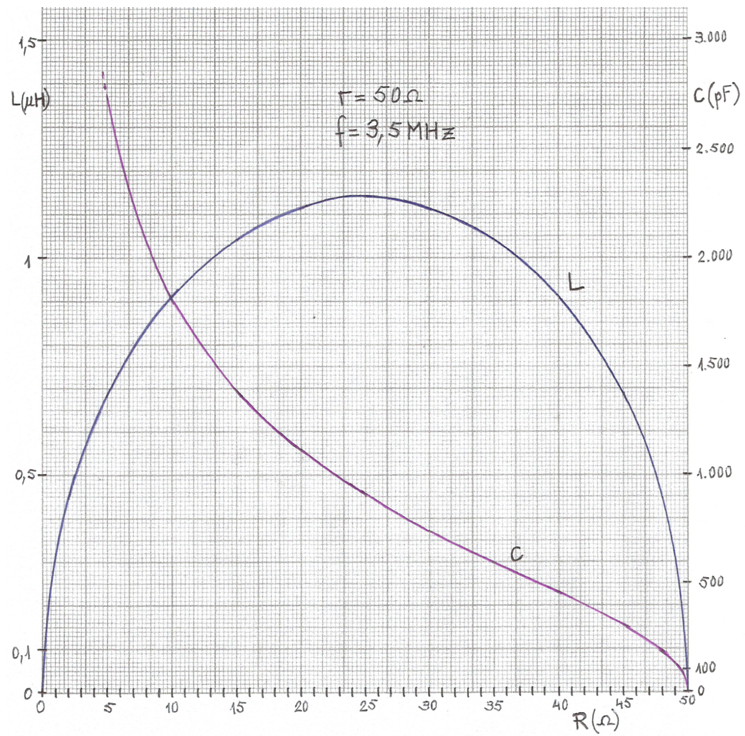
Igual com s'ha fet abans, anem a trobar les fórmules de L(R) i C(R) per a r = 50 Ω i f = 3,5 MHz :
fig. 17
Observació: Les diferències d'aspecte d'aquestes gràfiques respecte a les de la fig. 13 es deuen a què en aquestes el màxim valor de R és de només 50 Ω per la qual cosa l'eix d'abscisses s'ha graduat a escala lineal.
Igual que per al cas anterior de R > r , com que els valors de L i C són inversament proporcionals a la freqüència, per trobar aquests valors a altres freqüències només cal aplicar aquesta proporció inversa. A la següent taula de valors s'indiquen, per a R = 15 Ω , els valors de L i C a les freqüències de 1,8 MHz, 3,5 MHz, 7 MHz, 10 MHz, 14 MHz, 18 MHz, 21 MHz, 25 MHz i 28 MHz . En definitiva, el parell de gràfiques de la fig. 17 i la taula són suficients per determinar els valors de L i C per a qualssevol valors de R i de f .
Igual com es va fer en el primer muntatge, abans de muntar el circuit caldrà comprovar amb l'analitzador el valor de la inductància i el marge de freqüències que aquesta admet. Quan al condensador, a la freqüència de 14 MHz la longitud dels seus terminals introduiran un cert valor d'inductància paràsita la qual cosa, però, no és cap problema ja que es pot compensar variant lleugerament la capacitat respecte del valor teòric previst.
L'antena ressonat s'implementa amb una resistència de pel·lícula de grafit de 15 Ω .
Seguint una planificació de muntatge com el de la fig. 14, la fig. 19 és una fotografia d'aquest.
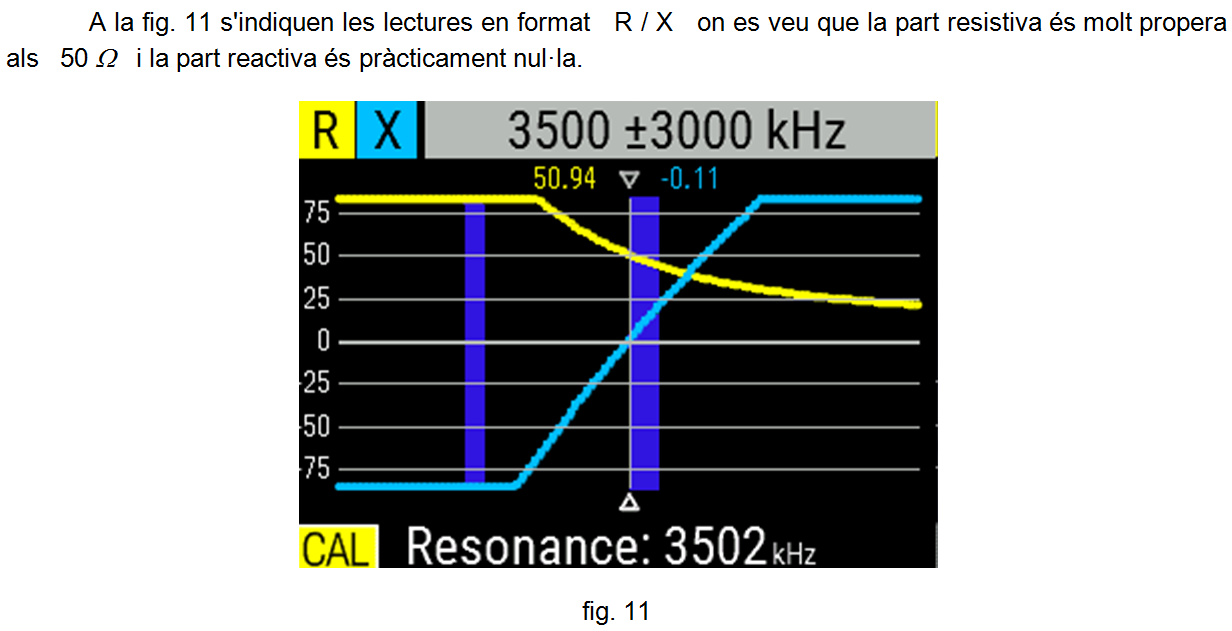
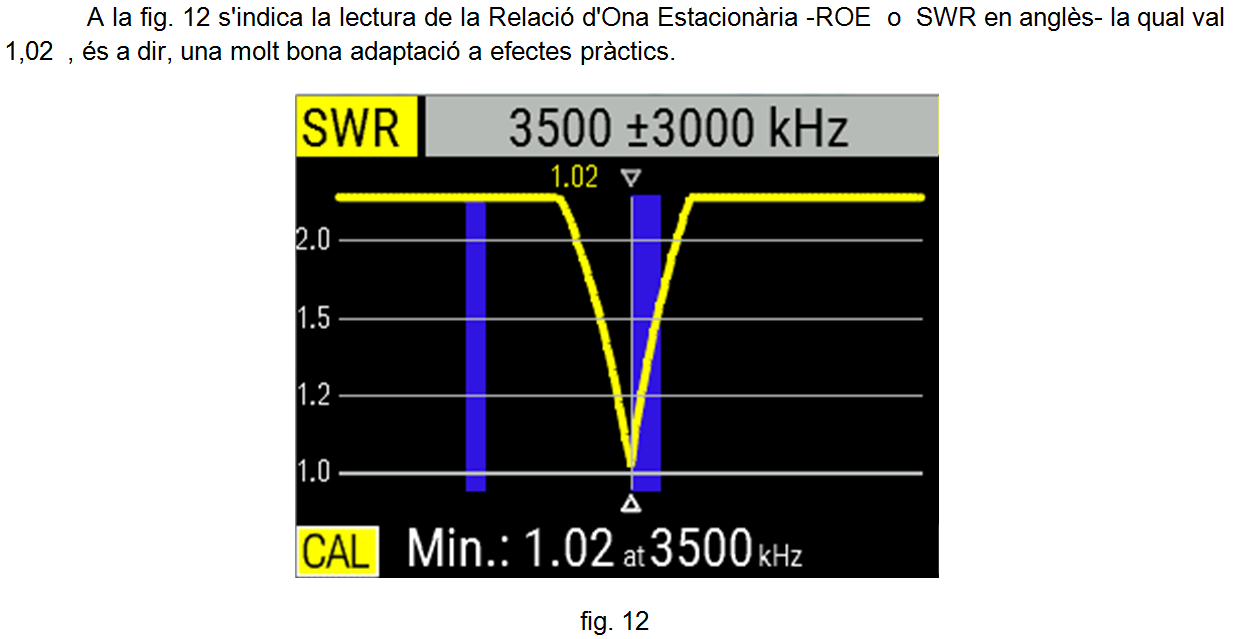
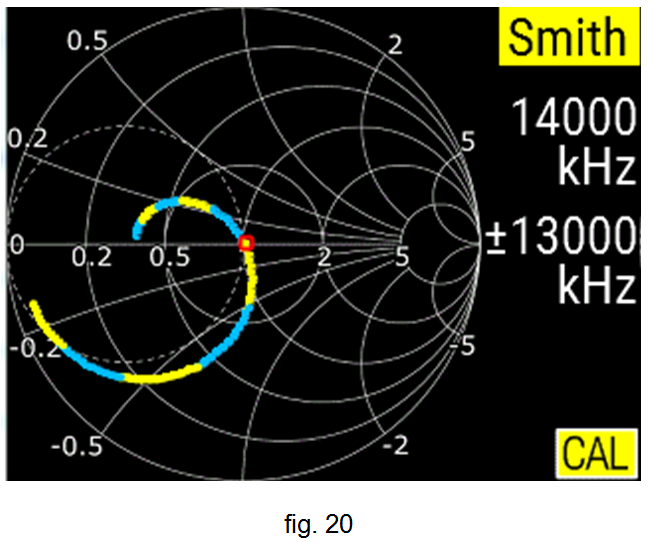
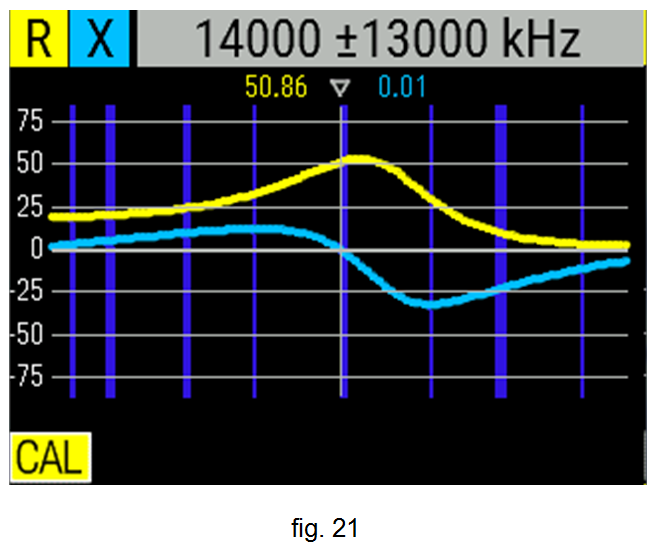
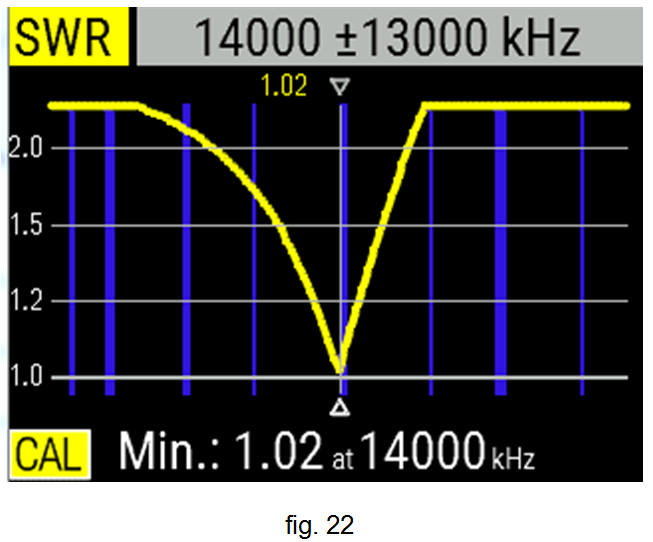
Ajustant adequadament la capacitat del condensador variable, a les fig. 20, 21 i 22 es veu la bona adaptació obtinguda emprant els diferents formats: carta d'Smith , R / X i SWR , respectivament.